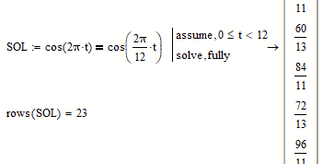Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
A simple challenge
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A simple challenge
Here is a simple math challenge for you. Solve with MathCAD!
On a regular 12 hour clock, how often does the minute hand pass the hour hand?
(Hint: The answer is not 60 minutes.)
Edit: I'm looking for the amount of time it takes for the minute hand to pass the hour hand.
I will post the solution in 1 week. Kudos abound!
Solved! Go to Solution.
- Labels:
-
Puzzles Games
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Edit: I'm looking for the amount of time it takes for the minute hand to pass the hour hand.
That depends on how thick the hands are 🙂
I guess that you mean the time between one pass of hands and the next one, right? I already wrote in an answer above that its exactly 12/11 of an hour. At least if we assume that the hands move continually and not stepwise 😉
@PG_10214301 also mentioned that it happens 11 times in a period of 12 hours which also makes for an interval of 12/11 hours.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@KevinFinity wrote:
Here is a simple math challenge for you. Solve with MathCAD!
On a regular 12 hour clock, how often does the minute hand pass the hour hand?
(Hint: The answer is not 60 minutes.)
Since you are asking for a number, the solution cannot have the dimension "time" anyway 🙂
Also you sure mean "during a time period of 12 hours".
Anyway - challenge accepted. Lets use Mathcad 15 to simply watch and count (and stop before we reach 12:00):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A similar question comes to my mind now:
If you exchange minute and hour handle so the the smaller hour handle now makes a full turn in 60 minutes, most of the time the handles will be in a position which does not show a valid time. How many times in a period of 12 hours the handles will show a correct, possible time?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Very interesting!
The answer to Werner's question is "as the hands of the two clocks mark the hour positions, starting from 12 o'clock thru 11 o'clock, eleven times in twelve hours."
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe I wasn't clear enough describing the problem. It was not meant that the clock with the exchanged hands shows THE correct time. This would be the case when the hands pass and so would yield the same answer as the original question.
What I had in mind was that this clock with a large hour hand and a small minute hand will have most of the time its hands in a position which would never occur on a "normal" clock and someone watching would immediately(?) realize that its not a standard clock. But sometimes in the period of 12 hours the hands would be in a position which could be a correct time and someone watching may not notice that the hands are exchanged (he may notice that the time is not correct, though).
Of course when the two hands pass we have a correct hand position and we already know that this happens 11 times in 12 hours. But there are also other hand positions where the clock with the exchanged hands shows a correct time. So the solution sure has to be quite greater than 11.
Here is an example of a hand position which ressambles a correct time no matter how the hands are exchanged:
BTW, an example for a clock where the hour hand is larger than the minute hand is the clock on the clock tower in Graz. Originally it had only one (large) hour hand, the smaller minute hand was only added later.
https://cdn.pixabay.com/photo/2020/02/23/21/30/graz-4874700_1280.jpg
https://www.blounge.at/wp-content/uploads/2013/03/uhrturm-graz.png
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"What I had in mind was that this clock with a large hour hand and a small minute hand will have most of the time its hands in a position which would never occur on a "normal" clock "
I'm having trouble envisioning a set of hand positions on a clock that wouldn't happen normally at some point in a twelve hour period. Please give me an example.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Fred_Kohlhepp wrote:
"What I had in mind was that this clock with a large hour hand and a small minute hand will have most of the time its hands in a position which would never occur on a "normal" clock "
I'm having trouble envisioning a set of hand positions on a clock that wouldn't happen normally at some point in a twelve hour period. Please give me an example.
You can't demand an arbitrary hand position because the position of both hands depend on each other, Whenever you move one, the other has to move accordingly. The minute hand moving 12 times faster than the hour hand. So every position you set the hour hand to forces one and only one position for the minute hand.
Lets say its 9:00 'o clock and now you exchange the two hands.
This position can never been seen on a regular watch (unless its broken and needs a repair).
The very same applies to 4:30 and an infinite number (most) of other times
But there is a finite number of times where exchanging the hands results in a valid clockface.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, the contest seems to be over so its time to solve my additional riddle, too.
The interesting part is that its very similar to the original question.
This puzzle was probably printed for the first time around 1880 and exists in different versions. In one of them a watchmaker has mistakenly installed two identical hands and the question is how often within 12 hours one does not know what time it is (because the position of the hands allows two valid interpretations). Here you would have to subtract the 11 positions where the hands are on top of each other (the original problem in this thread) from the solution to the problem as I formulated it here.
Of course, the task can be solved in many different ways (periodicity, systems of equations, ...). A very elegant approach goes back to the mathematician David Gale (https://de.wikipedia.org/wiki/David_Gale_(%C3%96konom)). He introduced a fictional third hand that moves twelve times as fast as the hour hand (which in turn moves 12 times as fast as the minute hand). And he went on to explain that a valid position of the reversed hour/minute hands is always found when this third hand and the hour hand are on top of each other. This means that the task is essentially traced back to exactly the one that was initially set here in the thread and one can analogously consider that such a hand position is always obtained at intervals of 12/143 hours. So within 12 hours there are 143 valid hand positions - here they are (I couldn't resist):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Added the display of the times in the animation and attach the MC15 worksheet:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, the question is "how much time does it take?"
I like your animations, though. You get the answer precisely for all times.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@KevinFinity wrote:Here is a simple math challenge for you. Solve with MathCAD!
On a regular 12 hour clock, how often does the minute hand pass the hour hand?
(Hint: The answer is not 60 minutes.)
I will post the solution in 1 week. Kudos abound!
The easiest answer I can give is based on the first twelve hours of a clock face (I'll double it at the end).
For each revolution of the minute hand, the hour hand moves one twelfth of the trip around the face, or 30 degrees. This however is assuming the same starting point on the minutes for each revolution but this is not so. Ultimately one revolution of the twelve hours must be subtracted due to the hour's constant transit around the face. This gives us eleven (11) times in 12 hours where the hands will coincide.
Double the eleven to get the value for a 24 hour period which is 22.
(12–1)*2=22
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You're correct, but that's not the answer I'm looking for. I apologize for how I worded the question originally. I'm looking for the precise amount of time it takes for the minute hand to pass the hour hand.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
On 'regular clocks' both hands move stepwise. This is most obviously shown by the 'seconds' hand, but also the minutes and the hours hands move stepwise, though it may be with very small steps.
Now the speed with which each hand turns to the next step is unspecified. How 'precise' do you think you can get the time?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
On 'regular clocks' both hands move stepwise.
I won't call the Seiko Springdrive not being "regular", but of course its rather unique. AFAIK its the only watch world wide with a real continuous hand movement.
Many mechanical watches have a seconds hand which moves stepwise in 1/4 seconds steps which looks quite fluent but still is not continuous, of course.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Simple problem; simple answer:
(This could be animated in 15!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Fred_Kohlhepp wrote:
Simple problem; simple answer:
Maybe not that simple 😉
Your reply is missing the actual answer to "how often".
Furthermore only every second point of intersection is a valid solution!
12 of those 23 solutions are not valid!
E.g. the "solution" t = 12/13 hr = 55.385 min corresponds to 00:55:23.077.
At this time the handles do not pass but are mirrored by the vertical
The times we are looking for simply are all multiples of 12/11 hours.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your reply is missing the actual answer to "how often".
The times we are looking for simply are all multiples of 12/11 hours.
really?
But you get credit for a really nice animation!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
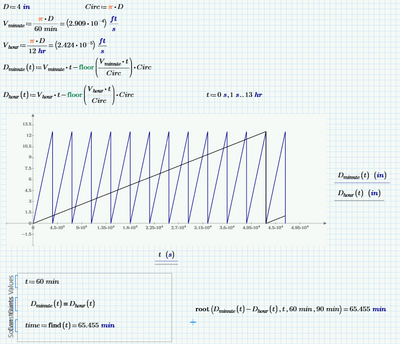
Yes, you showed a correct numerically arrived at solution for the time between one pass of the two hands and the next.
But the OP initially asked for "how often" (only now he changed it to "looking for the amount of time") and my reply mainly was triggered by what you wrote in the sheet/picture: "the question is merely when do they next intersect". And the very next point of intersection after 0:00 would be a wrong one and you skipped it deliberately without any further mentioning and hunted for the next which is a valid one 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You got the correct answer. I like your graph and your method, but Werner is also right- it contains too many solutions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Edit: I'm looking for the amount of time it takes for the minute hand to pass the hour hand.
That depends on how thick the hands are 🙂
I guess that you mean the time between one pass of hands and the next one, right? I already wrote in an answer above that its exactly 12/11 of an hour. At least if we assume that the hands move continually and not stepwise 😉
@PG_10214301 also mentioned that it happens 11 times in a period of 12 hours which also makes for an interval of 12/11 hours.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I thought it'd be fun to think of it as distance travelled instead of angle. Similar to Fred's otherwise.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello, everyone. Here is my solution. I modeled it as an infinite series and came up with the same results. It was very interesting to see the variety of different ways to get the same answer. Everybody thinks a bit differently, and that's what I wanted to see. Thank you all for participating.