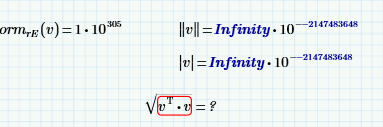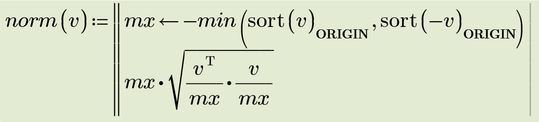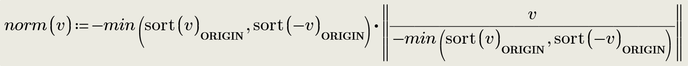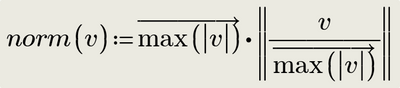Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Be careful absolute value function suffer from overflow and underflow for vectors
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Be careful absolute value function suffer from overflow and underflow for vectors
- Labels:
-
Programming
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting results in Prime 4.0 Express
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting, yes. I can understand the "Infinity" part (which is better than MC15's 0) as it may be the result of calculating the v^T*v first, which exceeds the IEEE limit, and the root of "infinity" is "infinity" again. But I am confused about the doubled minus sign in the exponent in front of the 2^31 (the largest 32 bit integer is 2^31-1, the most small is -2^31).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So, a bug?
Is the other way described a better norm function?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Modification to account for negative vector elements:
Same results
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
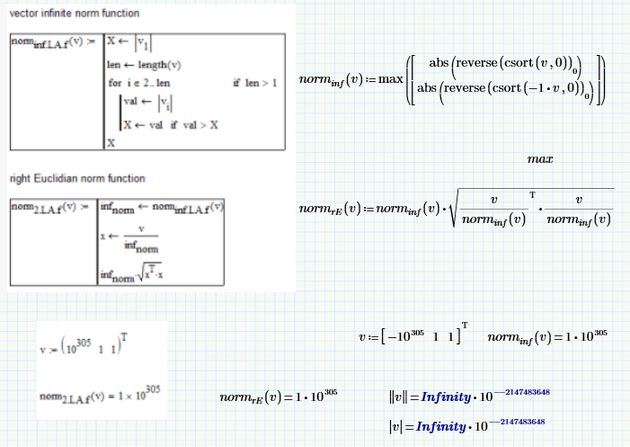
Your infinite norm yields wrong results for "normal" vectors which ifomenkos "infitite norm" does not, as it only triggers if the calculated absolute value of the vector is smaller (0 in case of MC15) as a single vector element.
Personally I don't like those workarounds where the norm of a vector is approximated by the largest absolute value of a single element. The norm of (10^300, 10^300, 10^300)^T is NOT 10^300, but rather about 1.7*10^300.
We all know about the limitations of the IEEE format so we should accept them and learn to live with them (or use different tools like symbolic math for special problems).
All that MC15 should do is to throw an error and not yield a wrong result. Thats also the reason I like Primes behaviour with the funny "infinte" result a bit more than Mathcads.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If we really need a workaround, here is one that seems to work OK
I used Freds idea to select the largest element, but used "-min" instead of "max" so I could avoid the calls to "reverse". As the function only deals with vectors I used "sort" instead of "csort".
For Express mx may be a separate function which is called multiple times?
EDIT: I guess this version should work in Express, too:
EDIT3: Here's the shortest version, which also works in Express:
All those workarounds should work in real Mathcad, too.