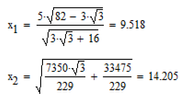Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
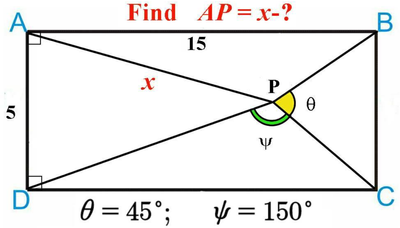
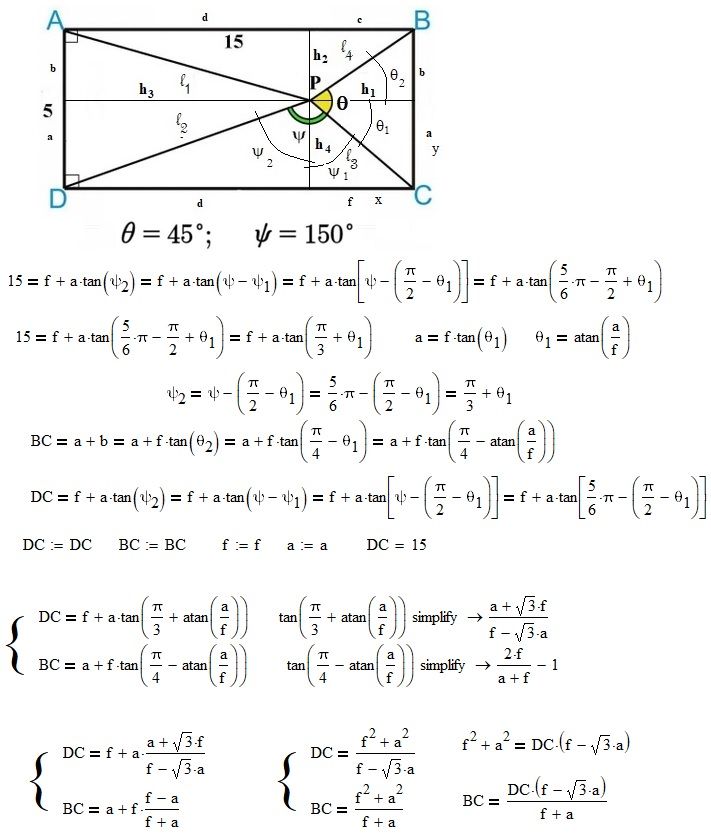
Best solution in Mathcad needed!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Who said that point P must be inside the quadrangle!
You didn't say anything at all when you "asked" - that was the problem with your question from the very first post you made. You just showed a picture where we could read "Find AP = x-?" Not AP with a straight line/bar over it, so we even can't say if the length of a line segment is meant or something else. We also don't know what the minus sign after x should mean - are you looking for the subtrahend of a difference? Luc noted the "missing" right angles resp. missin lengths which you later submitted.
So what could we do with that initial post of yours? As I see it we had just two options: assume the most obvious or reject the question as inadequate. Maybe the second variant would have been more appropriate?
Anyway, I look forward for you to show us correct symbolic solutions and of course an animation showing all possible solutions 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm playing with some pieces of paper cut to appropriate angles and can't see anyway P doesn't fall inside of the box. But maybe I'm missing something. However, it does appear we all (perhaps foolishly) assumed this is a 2D problem. I believe 3D opens up some additional answers, or else maybe it's now undefined.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@DJF wrote:
I'm playing with some pieces of paper cut to appropriate angles and can't see anyway P doesn't fall inside of the box. But maybe I'm missing something. However, it does appear we all (perhaps foolishly) assumed this is a 2D problem. I believe 3D opens up some additional answers, or else maybe it's now undefined.
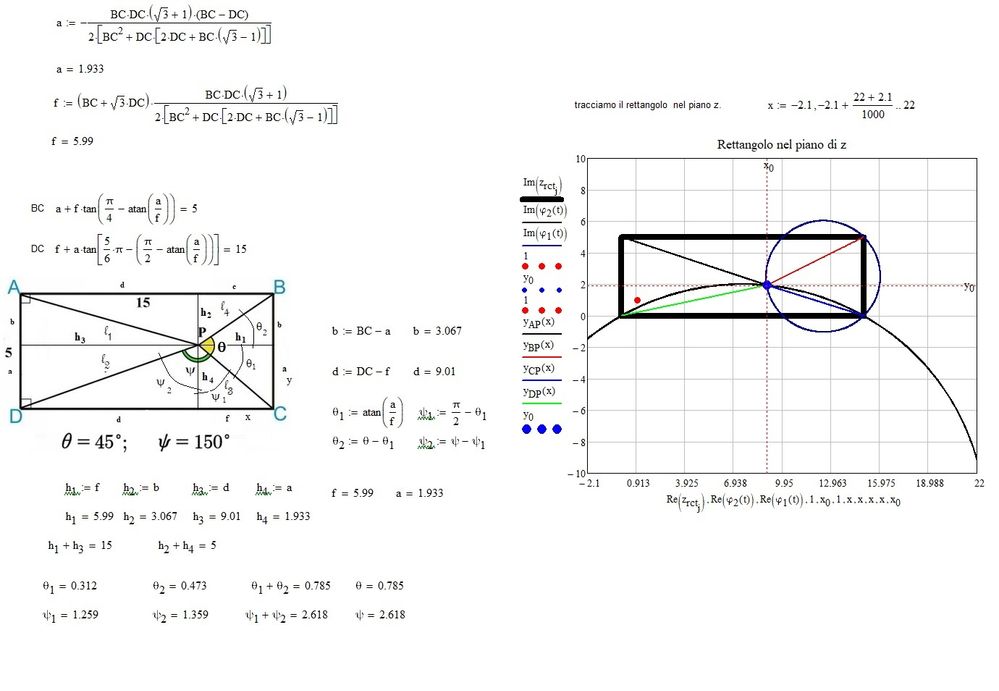
If you drop the constraint that P should be inside the rectangle (or quadrilateral in the extended problem version with variable length CD) a second solution is possible. Only constraints are now the two angles psi and theta (without orientation!). There is NO second solution in the range for CD which Valery had highlighted in his plot, but accepting points outside of the rectangle/quadrilateral there are two solutions for CD greater than approx 13.66 (exact: 15-5*cot(75°)). The range 0<CD<13.66 seems to be exactly the range where Valery's last attempt did not come up with any solution. In fact here the solution is unique.
See for example in the picture the second solution for the initial problem with the rectangle. While the solution point inside the rectangle had the approx. coordinates P(9,010 / 1,933) the solution outside has the coordinates P2(12,868 / -1,016).
The two solutions for x in this case are
If you want to interpret the thing as a 3D task, you'd have to be more specific as to what the problem exactly is.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
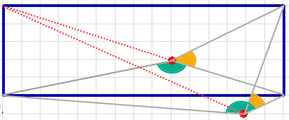
AB=CD - we have not one but two solutions - two points (see the picture above)!
AB not =CD - we have not one but two solution - two curves!
Sorry - no time to solve this problem - I must solve others problem!
Help me please if you have time and wish!
The Ghost of solution
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AB=CD - we have not one but two solutions - two points (see the picture above)!
Thanks for pointing me to it, but it was me who made and posted that pic, so I know it 😉
AB not =CD - we have not one but two solution - two curves!
If if do not demand that P should be inside the quadrilateral, then yes. But its not as you show in your picture. As I already wrote in my post above, there are only two solutions if C>13,7 (approx., exact expression is given in my post above). For 0<CD<13,7 there is only one single solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A different approach to the problem, but with the same previous results:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
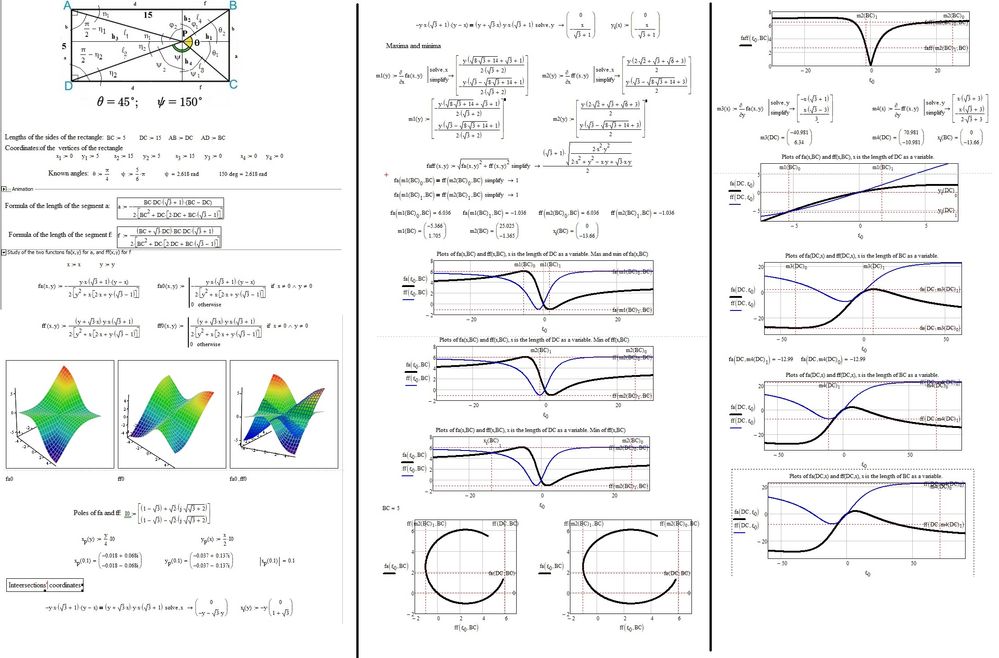
Study of the problem. Possibility of freedom of movement of point P (x0, y0).
I should say something about the possibility that the point P can move at least around the rectangle. From this analysis it seems possible. It requires further study.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Looks interesting - could you please elaborate on what the various plots in our sheet show?
As far as I see your functions are dependent on variable length CD and variable length BC.
In the (extended) question so far AB and CD were still parallel and so BC could be calculated based on CD.
Does your sheet extend the problem further to even more general quadrilaterals?
As far as I understood the pending question so far is a about the position of P and the distance AP when CD is changing (with DC parallel to AB).
Which problem do you study in your sheet?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is the study of the trend of the two segments, a and f, varying the dimensions of the rectangle sides simultaneously (the two surfaces) and of one side at a time (graphs).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@-MFra- wrote:
It is the study of the trend of the two segments, a and f, varying the dimensions of the rectangle sides simultaneously (the two surfaces) and of one side at a time (graphs).
Not sure if i understand correctly.
Do you really mean rectangle? This would mean AB=CD and AD=BC as in the initial question.
Given theta and psi there are just two distinct solutions for the point P - one inside and one outside of the rectangle as shown in a post above.
As you wrote about the point P moving around the "rectangle" I guessed you meant a more generic quadrilateral where A, B and D are as given initially but C can be anywhere in the plane as you made all dependent on DC and BC. If this assumption of mine was correct this still would mean that P can only be on a circle (better: arc) through B and D, since the angle PBD is always 165 ° (for P inside the quadrilateral, otherwise 105° and two other arcs).
I also don't see how you would define a and f if ABCD is not a rectangle.
Basically I don't see which quantities of the original question are fixed for you (guess A, B and D with their respective length AB, etc. and also angles psi=DBC and theta=BPC) and which are variable.
A sketch (if ABCD is not necessarily a rectangle) would certainly help me to understand what you are showing, I guess.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No answer - that's a pity!
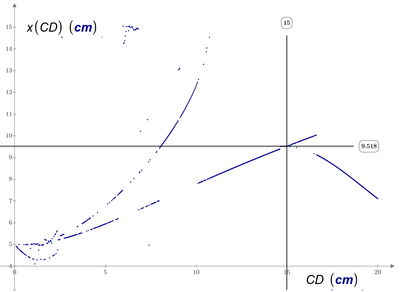
But no matter - anyway, to conclude for what ever it may be worth, here is a small animation made a few days ago, which shows the position of the possible solutions for P and the graphs of the distance functions at variable distance CD.
have fun!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hooray! I won! I believed in Werner and made a bet on him in the bookmaker's office! He came first to the finish, sorry, to the solution. But this is an intermediate finish! We remove one more restriction - the trapezoid lies not on the plane, but on a sphere with radius R ![]()
- « Previous
- Next »