Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Center of gravity
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Center of gravity
Hello,
Has somebody an Idea, how to calculate the center of gravity (zs1) in zylindrical koordinates (The boundarys of the 3-Integrals are not really clear for me)?
See attached Files-sheet two of Kugelspeicher.mcdx.
Thank you very much!
Volker
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

Okay.
- The 2 pi is the integral around the angle (full circle.) There is no dependence of radius (or height) with azimuth, so a true integral with angle is not required. (That's why there are only two integrals to get volume.)
- The variable "s" is a variable of integration. It does not appear outside the integral. The inner integral above is the integral over the radius. the limits of integration (for V3) are the radius of the center pipe (d/2) to the outside of the sphere (defined by the function r(z):

- The outside integral is the vertical integral (z), the limits of integration are the bottom and top of the water.
This is equivalent to your integral above except that the outer bound for radial integral is a function of height "rr(z).

Your integral has height as function of radius; I don't know how to write those functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I get CG's of odd shapes by integrating. Attached is integration in cylindrical coordinates.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred, I understand the integration of zylinders, etc.
But this is not the answer of my question.
I want to have the integration limits of the Integral concerning to the sketch:
This is a water-reservoir (shaded Area) of whitch i only want to know the integration limits for Integration to get the Volume.
Thank you

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry!
Mis-read the problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No Problem!
What is "s" in your formulas?
can you tell me the geometrical meaning of this?
It would be better for me to understand when you use the same parameter names whitch are given in the sketch.
Zylindrical koordinates:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

Okay.
- The 2 pi is the integral around the angle (full circle.) There is no dependence of radius (or height) with azimuth, so a true integral with angle is not required. (That's why there are only two integrals to get volume.)
- The variable "s" is a variable of integration. It does not appear outside the integral. The inner integral above is the integral over the radius. the limits of integration (for V3) are the radius of the center pipe (d/2) to the outside of the sphere (defined by the function r(z):

- The outside integral is the vertical integral (z), the limits of integration are the bottom and top of the water.
This is equivalent to your integral above except that the outer bound for radial integral is a function of height "rr(z).

Your integral has height as function of radius; I don't know how to write those functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, now we get closer to the problem.
Can you please post your MathCad file?
Is rr (z) equal to z (r)?- it confuses me.
Inner limits are d/2 and r (z), is that right?
You solved my problem.
I guess i had the wrong sequence in the integrals.
First "r" then "z" and at last "phi"
The equation:
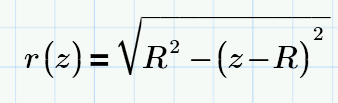
I can't see the geometrical meaning, can you please explain in a sketch?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
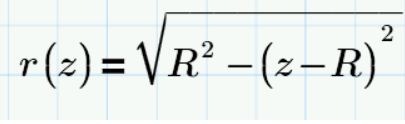
Solves for radius as a function of z, vertical position from the bottom of the sphere. (Pythagoras' Theorem.)
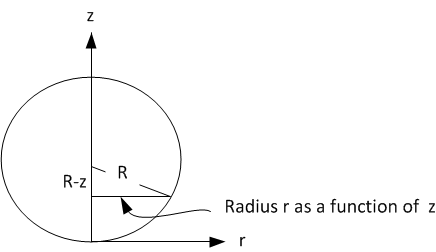
Height as a function of radius z(r) isn't helpful because there are two values of z for each r, while there is only one radius for each z.
The file is attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery,
sorry, but this doesn't solve my problem.
I wanted the correct limits for the Integration of a volume concerning to the upper shown sketch in my origin post.
Yes-It is necessary for finding the center of gravity
Thanks, anyway
Volker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Added
Z centers of gravity on page 2
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
Thank you for your help.
I changed something in your File: I replaced rr(z) to r(z) because rr(z) is confusing me.
Volker


