Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Cone, plane, ellipse
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cone, plane, ellipse
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes,
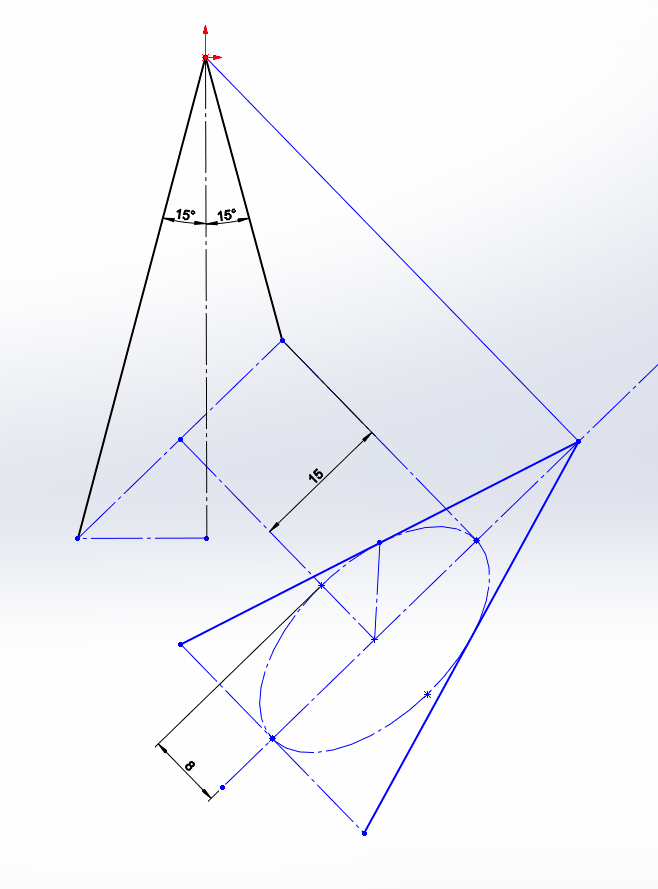
here is example when a=15, b=8 and alpha=30 degree...
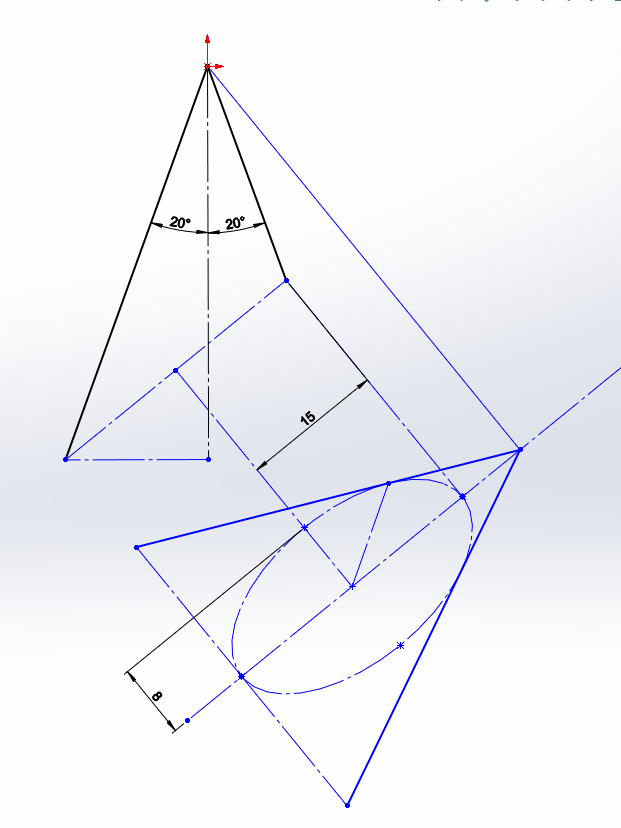
..and when alpha changes to 40 degree
Observe that auxiliary view is normal to cutting plane and does not show real cone angle.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
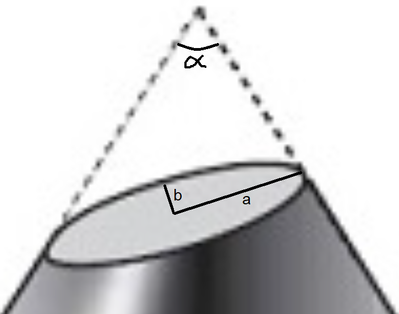
a & b are not sufficient to define alpha.
No mather what alpha you have, you can allways slice cone to obtain ellipse with dimmensions a & b.
/Avdo
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks!
For a of a circular cone too?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes,
here is example when a=15, b=8 and alpha=30 degree...
..and when alpha changes to 40 degree
Observe that auxiliary view is normal to cutting plane and does not show real cone angle.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks!
I suspected it. But I always want to check!
When I was in school, I drew something around 1000 triangles, measured their angles and made sure that their sum is 200 degrees.
Just kidding! 180 degrees!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice,
Now: is it possible to prove, or dis-prove, that one of the two focal points of the ellipse lies on the axis of the cone?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fine idea!
Add condition of the problem!
One of the two focal points of the ellipse lies on the axis of the cone.
PS
New year tree for our problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Fine idea!
Add condition of the problem!
One of the two focal points of the ellipse lies on the axis of the cone.
Mission impossible (if we still are talking about a circular cone).
The focal points are where the Dandelin spheres touch the plane.
-> https://en.wikipedia.org/wiki/Dandelin_spheres
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Theoretically there is one trivial solution to the problem!
One focus is on the axis if other focus is on axis too 🙂 lol
observe that circle is only special variant of the ellipse when a=b=r
otherwise it is allways offset from cone axis to the focal points.
/Avdo
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ptc-5737066 wrote:
...
otherwise it is allways offset from cone axis to the focal points.
Which needs to be proved.
One way to do so is by the Dandelin spheres - if of them should touch the plane in a point on the axis, the plane has to be horizontal and the intersection is a circle.
You sure know that the center of the ellipse is not on the axis as well (unless in the case of a circle).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes!
When Dandelin spheres touch eachother both focuses and ellipse center melt into touch point onto axe and ellipse becommes circle.
Since that no focus points nor ellipse center can coincident with axis.
Axis is allways intersecting the line between two focuses splitting it in one longer and one shorter part.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
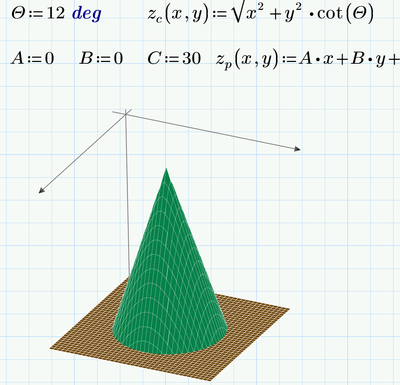
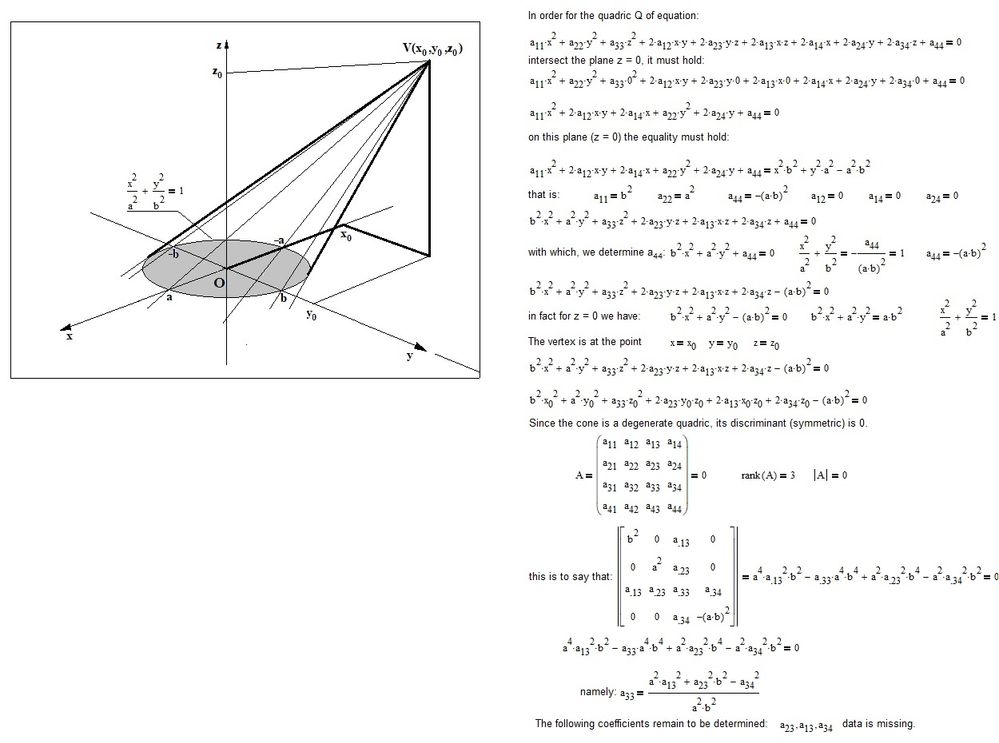
Hi,
With the use of analytical geometry and with the data available, this is all you can do:
Happy New Year.
F. M.