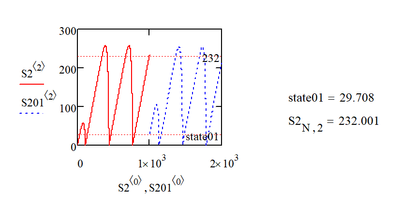
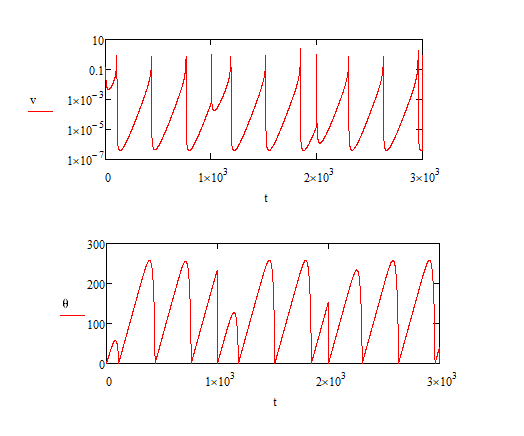
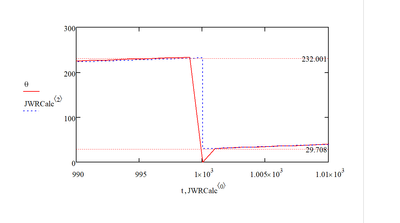
The conditions for the solution of the problem:
dxdt=F(t,x(t)),x(t0)=x0,dxdt=F(t,x(t)),x(t0)=x0,
to exist and to be unique is that F∈C0t,xF∈Ct,x0 and Lipschitz continuous for t>t0t>t0. Then, the solution of the problem is given by:
x(t)=x0+∫tt0F(t,x(t))dtx(t)=x0+∫t0tF(t,x(t))dt
Note that for the function FF to be integrable in t>t0t>t0, it must contain finitely many discontinuities so x(t)x(t) remains continuous in t>t0t>t0 whilst, otherwise, x′(t)x′(t) may not, in general.
As an example, consider the problem:
x′(t)=H(t−1),x(0)=0,t>0.x′(t)=H(t−1),x(0)=0,t>0.
Its solution is then given by:
x(t)=(t−1)H(t−1)x(t)=(t−1)H(t−1)
which is continuous but not differentiable at t=1t=1.
Cheers!