Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Electronic boards design: assessment of the component tolerances
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Electronic boards design: assessment of the component tolerances
I'm using Mathcad prime 2.0 (express version) but the question can be solved using premium version.
I would use Matcad to study the effect of the tolerance of the components I choose on the electronic circuits that I projected:
suppose, for example, you have a resistive divider formed by R1 and R2 powered from Vcc ..
we know that the voltage of R2 is:
f(Vcc, R1, R2): = (Vcc / (R1 + R2)) * R2
I want to ask Matcad which values (maximum and minimum) can f() assume if
R1 has a nominal value of 1000, with a tolerance of 1% (therefore can have a value from 990 to 1010)
R2 has a nominal value of 2000, with a tolerance of 1% (therefore can have a value from 1980 to 2020)
The right way would be to use the function minimize () but I can not figure out how to properly set up the command
Thank you
Solved! Go to Solution.
- Labels:
-
Physics
- Tags:
- engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Find attached a version which (I hope) works in Prime Express, too.
EDIT: No, it can't work in Express as Express does not allow for programming
It uses two custom function: The first creates a vector of values given nominal value, tolerance and number of intervals. The second routine was a bit tricky to write. It takes a function and a vector of arguments and cycles through all the arguments finding max and min. The function has to be one with only one argument being a vector. This is necessary mainly because we are not allowed to write functions with a variable number of arguments.
Hope the attached sheet helps. You can apply this method to more complicated expressions with more than only two restistors, too.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I fear, if he is only using the Express version of Prime he will not be able to read that worksheet and even if, he will not be allowed to use solve blocks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a version in Mathcad Prime 2.0. Minimize and Maximize are premium functions, and require a license. Use a trial license.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks for the answer, I get this work using a 30days trial version, thankyou very much
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
I take your worksheet for electronics computing. It works well, but i've a problem when the equation is too long...
With the first equation, result isn't diplay because no solution are found (for R265).
But for the second equation with "*" instead of "+" a solution is found.
File with Mathcad 2.0 (premium account) :
http://sendbox.fr/pro/josjvto20jfs/tolerance_FULL_V3.mcdx.html
http://www.filedropper.com/tolerancefullv3
I try to define TOl and CTOL variable with value from 0.001 to 1, but no convergence (no solution).
have you got an idea for the problem?
=> Maybe this exemple could be help you to help me in order to find the problem
1) In green : equation + 0 => Convergence is OK
2)In red : equation + 0.1 => Convergence is NOK
Why?
Thank You, Emilien
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Did you try to change the guess values?
I looks like you should omit R.464 completely, I can't spot in in your expression.
You may consider attaching your file directly here - to get the option to attach files you have to chose "Use advanced editor" at the upper right of the posting window.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I just had look at one of the sheets you provided.
You have a unit mismatch problem in your function f(). You have to type 12V instead of just 12 to make it work!
It seems to be the same problem in the last pic you provided - add 0.1V instead of just 0.1. By adding + 0 Prime (sometimes) guesses the correct unit itself and thats the reason it works in your screenshot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much, it works when I add the "V" units.
And thank you for the tips in order to attached a file.
Emilien
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
happy new year Everybody! ![]()
I begin the new year with a problem on my Worksheet.
For a value of a capacitor, constraints aren't respected. I don't understand why.![]()
All computed value are not optimised when I add this capacitor.
No errors appears.
Function on my worksheet :
Find a minimize :
Result
We see that, they are no optimisation on any component (value are in the middle) and value for C127 are not between (1nF -150pF < C127 < 1nF + 150pF).
If a put a fixed capacitor value (1nF) on the function :
Other components in this case are "optimize" in order to find the minimum of the function.
I don't find why, when a put the C127 capacitor, constraints are not respected? Where is the mistake?
File is included in the message ![]()
Thank You, Emilien
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When using a solveblock with Minimize constraints are NOT hard constraints. Prime tries to find an overall good fit - you may not get the absolute minimum of your function and constraints may not be fully respected. You may weight the one or the other constraint by using a factor like the 10^3 in the example below. If the constraint isn't respected, the absolute error gets bigger that way and so Mathcad tries to to a better job. There is no guarantee that all constraints will ever be respected.
In case of your function the capacitor C127, which is a factor of the function, has a very big influence on the outcome of f_temp(). The absolute minimum for f_temp (which is negative infinity) is achieved if C127 approaches negative infinity. Its only your constraint which stops Prime from assigning a value like -10^23 to C127.
So Mathcad primarily "plays" with C127 as the other variables don't affect the outcome of the function that much.
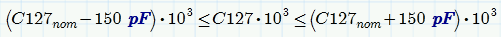
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for your answer.
But, If I change the factor from "1" to "10^3", C127 will be at the good value for a minimum f_temps function, but other components will not optimized.
With C127 capacitor from 900pF to 1100pF :
If a had a factor of "1.10^3"
f_temps = 3.85µs (C127_min = 900.39pF)
If I don't had any factor :
f_temps = 2.79µs (C127_min = 653pF)
If a replace C127 by 900pF with fixed value :
f_temps = 2.575µs
This one is apparently the minimum of f_temps function.
Computing results are not OK like you say. What is the best solution for my problem?
Is it possible to give only 2 value for C127 (C127_min and C127_max) in order to simplify computation?
Can I force "Prime" to compute with more precision the minimum of the function?
Thank you
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What is the best solution for my problem?
Can I force "Prime" to compute with more precision the minimum of the function?
As already said, the problem arouses mainly from the way your function is built. You get (with all the other variables staying constant) the minimum when C127 is at its minumum. So the best solution seems to set C127 at its minimal value (850 pF) manually and let Prime optimize the rest of the variables which seems to work.
The algorithm Prime uses is, as I guess, Levenberg-Marquardt. In MC15 and below we were able to chose from different algorithms but in Prime we miss this feature. But I guess it wouldn't help in this situation anyway.
Another approach to that kind of problem is brute force. Thats the method I posted some times ago in this thread (its just the posting below, file is MinMax.mcdx). You have to setup a function with a 11x1 vector as argument and create vectors of values for all the eleven variables used. Then the routine will combine every value in each vector with all the others and returns minimum an maximum of the function along with the parameters to get there. Depending on the number of variables in play and the number of values for each variable this may take quite some time to finish. Using a coarse grid you may miss the real minimum, using a much finer grid it may take a lifetime to finsh. Working with 100 values for each variable would mean that your function has to be evaluated 100^11=10^22 times - not sure how long it would take Prime to do so, but I guess its not acceptable, but then, you may give it a try.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Find attached a version which (I hope) works in Prime Express, too.
EDIT: No, it can't work in Express as Express does not allow for programming
It uses two custom function: The first creates a vector of values given nominal value, tolerance and number of intervals. The second routine was a bit tricky to write. It takes a function and a vector of arguments and cycles through all the arguments finding max and min. The function has to be one with only one argument being a vector. This is necessary mainly because we are not allowed to write functions with a variable number of arguments.
Hope the attached sheet helps. You can apply this method to more complicated expressions with more than only two restistors, too.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks for the answer, thankyou very much


