- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Equations for iso-lines (Larson-Miller constant)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Equations for iso-lines (Larson-Miller constant)
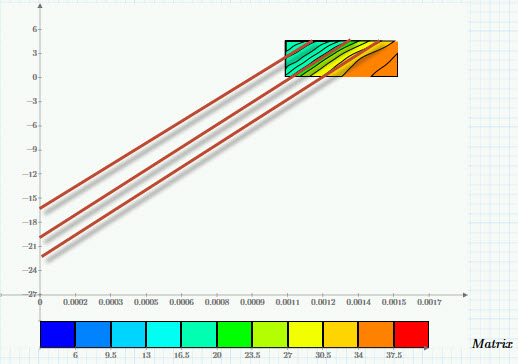
Hi all. Here's my question. I would like to be able to line fit an iso-line. Mathcad clearly can generate the data for the iso-line since it plots it on a contour plot. Is there a way to get the coordinates of the iso-line so that I can fit it to calculate the y-intercept? Or maybe there's a completely different way to solve this problem. Attached is the Prime 3.1 file and pdf that will explain what I'm after more clearly.
Basically I'm trying to generate the red lines I've overlaid here (with a paint program)
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I combined parts from Fred's and Richard's solutions to create my 'final' worksheet (attached). I appreciate all the help; I certainly learned a few tricks with this one.
Thanks again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, I can't open a 3.1 file. Assuming you are starting with data, you need to fit the data with a surface to get a function. I don't know anything about your data, so it's hard to suggest a function. Spline interpolation will always work, but is not necessarily the best choice. Then use a solve block to find the y value for given values of x and z.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,
PDF is included in archive file from above.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
dferry wrote:
Hi all. Here's my question. I would like to be able to line fit an iso-line. Mathcad clearly can generate the data for the iso-line since it plots it on a contour plot. Is there a way to get the coordinates of the iso-line so that I can fit it to calculate the y-intercept? Or maybe there's a completely different way to solve this problem. Attached is the Prime 3.1 file and pdf that will explain what I'm after more clearly.
Basically I'm trying to generate the red lines I've overlaid here (with a paint program)
Unfortunately, Mathcad doesn't actually generate the isolines. This is a function of the plotting 'component' and the values are private (there is a long, long, long standing feature request to make this information available from the plot).
However, Mathcad has a few ways of generating the isolines, the complexity of which will depend upon the nature of your function. As it looks fairly simple from the image, I'lll give an example of two methods (in Mathcad 15, but should port to Prime) using the root function and a solve block.

Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
Unfortunately, Mathcad doesn't actually generate the isolines. This is a function of the plotting 'component' and the values are private (there is a long, long, long standing feature request to make this information available from the plot).
However, Mathcad has a few ways of generating the isolines, the complexity of which will depend upon the nature of your function. As it looks fairly simple from the image, I'lll give an example of two methods (in Mathcad 15, but should port to Prime) using the root function and a solve block.
Ignore the above ... I've just read your pdf and it's a different problem.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I didn't realize there was also a pdf until Stuart posted. Could you please post your data in an Excel spreadsheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's the raw data and the data converted into the "Matrix' used for plotting.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here. Developed in MC15 and converted to Prime, because 3D graphs in Prime are lousy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad can do a multivariant regression.
you can create a function that fits your data with "polyfit."
You can see the coefficients with "polyfitc."
Short example attached. With this function, you should be able to extract C.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have just realized that what you are trying to do cannot work. You say "Larson-Miller considers that iso-stress lines intersect the y-axis at a constant point". However, to be able to extrapolate the isolines as straight lines to 1/T=0 (so T is infinite - seems strange to me) would require that the isolines are straight lines (or the points generated from them are in a straight line), which in turn means the surface is a plane. However, if the surface is a plane then the isolines are parallel, and will not meet at the y-axis (or anywhere else!). For isolines (i.e. contours) to intersect the gradient of the surface has to become infinite.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Try this. I'll leave you to fit lines through the data sets. I don't need to do that to tell you that they will not intersect at the y-axis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess I couldn't resist ![]()
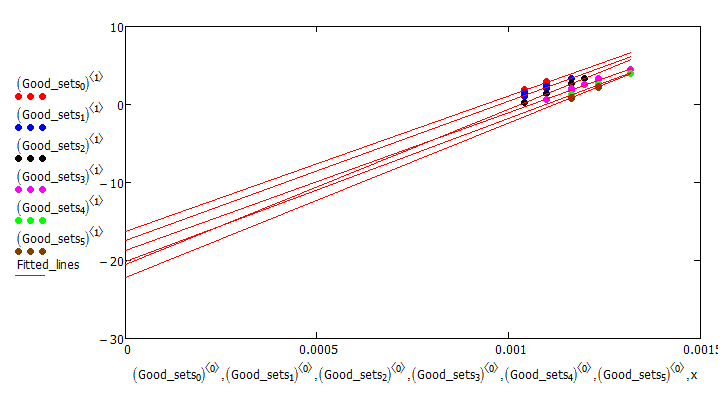
I suppose you could just take the average of the intersection values. Better than nothing perhaps.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Or, we could force a common intercept
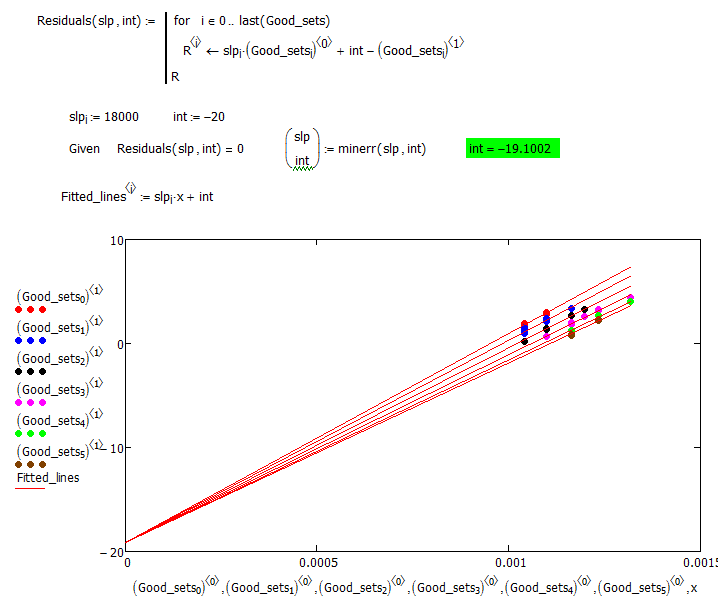
The fits still look reasonable:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard, it will take me a bit to absorb your files, but I'll comment on the intersection point. Yes, it's true that I'm not expecting a perfect intersection point for the various lines. Both the theory and the test data are imperfect. However, Larson-Miller is popular because it is very simple and accurate 'enough' for most purposes. It's an engineer's equation, not a mathematicians'. And it's simplicity is based on assuming a constant intercept. So, my efforts currently revolve around trying to be sure I can justify my choice of a constant. At worst, I just do a sensitivity analysis with the range in intercept these plots give me. Most people just use 20 and call it good.
Different materials display different trends in the iso-stress lines. If lines are parallel the Sherby-Dorn approach would be more accurate as it assumes parallel iso-stress lines.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Both the theory and the test data are imperfect.
Extrapolation of a function fitted to data is rarely a good idea, because data is never perfect, but if the theory is also only approximate, and the extrapolation is very large, then any result you get is subject to huge errors. Depending on how I analyze the data I can get an intercept anywhere from -15.5 to -19.2. But that's based on only four methods of analysis, so there's no guarantee the true intercept is within that range. Anywhere from the low teens to the low twenties would be believable.
Most people just use 20 and call it good.
That might be just as accurate, and a lot easier.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
Extrapolation of a function fitted to data is rarely a good idea, ....
Hi Richard.
The best extrapolation that I know is -273.15 °C. The worst, climate predictions (maybe are some kind of that). Don't worry, I don't believe to much in extrapolations.
Cheers.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I combined parts from Fred's and Richard's solutions to create my 'final' worksheet (attached). I appreciate all the help; I certainly learned a few tricks with this one.
Thanks again.


