Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Explain me please differents between...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Explain me please differents between...
Explain me please differents between cspline, pspline and lspline!
Can you send me please anyone about a code of those function.
Thanks
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
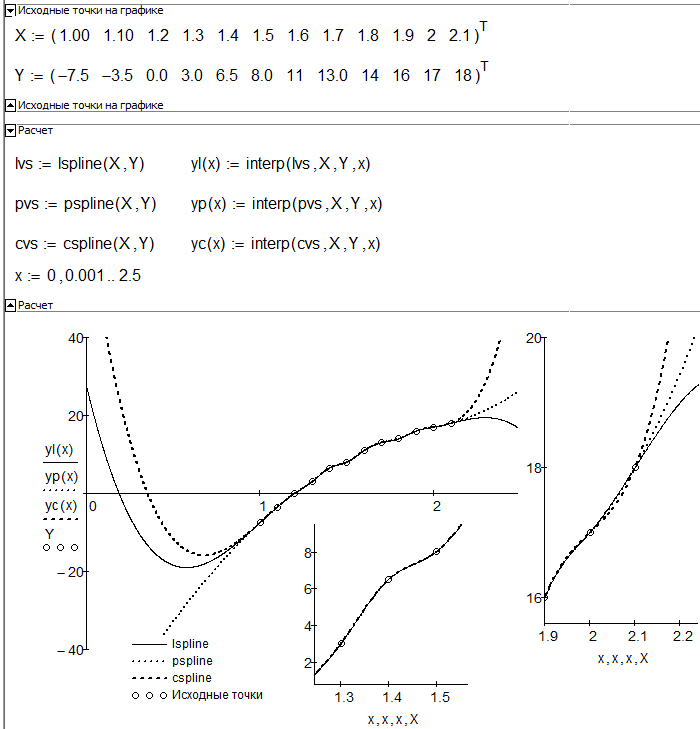
To clean up with a wrong interpretation I have read here some times - all three, lspline, pspline and cspline create cubic splines! The difference is the behavior at the endpoints. You can look up spline theory in any good math book so to keep it short, cubic splines interpolate a tabled function using a (different) cubic between each two tabled points and the goal is to have a continuous second derivative over the whole range covered by the tabled points - especially at the joints, too. The second derivative is linear interplated between every two points and so we usually get polynomials of third order, cubic splines.
But what about the second derivative in the first and last point of the table? We are free to choose any value we like and so we have different options.
One way is to set the second derivative at the endpoints to 0. This means that our splines have zero curvature at the ends - the endpoints being the inflection points of the last cubics - "linear" at the ends. This is what we get with lspline and the result sometimes is called "natural" spline.
A second way is to let the second derivative in the first point be the same value as in the second one and similar for the last two points. This means that the second derivative is constant at the end segments and our splines here are parabolas. Thats what we get with pspline.
The third way is to linear extrapolate the second derivative in the first point by using the second derivatives of the second and third points and similar at the other end. And this is what we get with cspline.
Because splines are not just a local interpolation but a global one, changing the behavior at the ends will also affect (sligthly) all cubics in between, too
For further reading you might find these articles interesting (apart from the usual literature on splines, B-splines, etc.):
http://www.chem.mtu.edu/~tbco/cm3450/cubicSpline.pdf
maybe in this context its also worth to look at the discussion and sheets (provided by jmg and Tom) here
interpolation cubic spline (2D)
or having a look at Tom Gutmans spline sheet here
Regards
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Werner!
One interesting picture: