Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
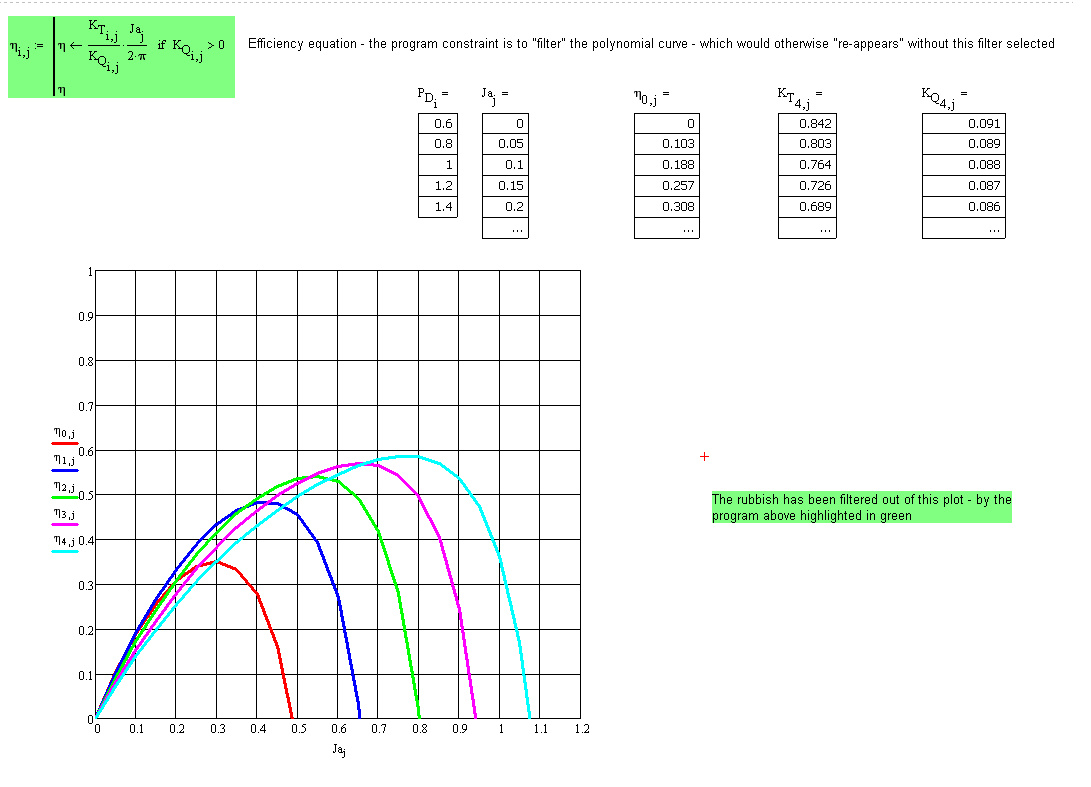
Filtering of "rubbish" from regression curves
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Filtering of "rubbish" from regression curves
Hi,
I have been given the polynominal regression coefficients for the torque, thrust, and efficiency curves - corresponding to different propeller pitch to diameter ratios. When I graph these curves - they come out fine - apart from the fact - that because they are polynomials - they "re-appear" - outwith the range of that particular curve.
So my question is - how can the "rubbish" be filtered out of these regression curves? If you look at the attached spreadsheet - you will see the efficiency curves - have a lot of rubbish - beyond the "curve".
So in essence - I would like to "stop" - the graph - once the "curve" has been displayed. I suspect - I need a program to do this - but I am unsure how to do this.
Look forward to your ideas.
Gordon.
Solved! Go to Solution.
- Labels:
-
Physics
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Inspired by Fred - here is another functional approach. Plotting is somewhat slow as the functions will try to determine the zero point for every call to the function.
The local approach using the sign of the derivative sure is quicker and works, as long as the type of function doesn't change much. It will certainly not work for eta.But then my way of using root to find the zeropoint is also limited to "good behaved" functions KT and KQ.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It depends upon how exactly you would define "rubbish". For instance thats what you eta1 looks like
How would you change the values in this vector? It woule be reasonabla that the length of the vector (as its part of a bigger matrix) should not be changed. So the "rubbish" values have to be changed in a way the corresponding points are not seen in the graph. One approach could be to keep the values constant as soon as the first value is negative. Don't know if this what you want, but it will look like this:
Look if the attached would help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner,
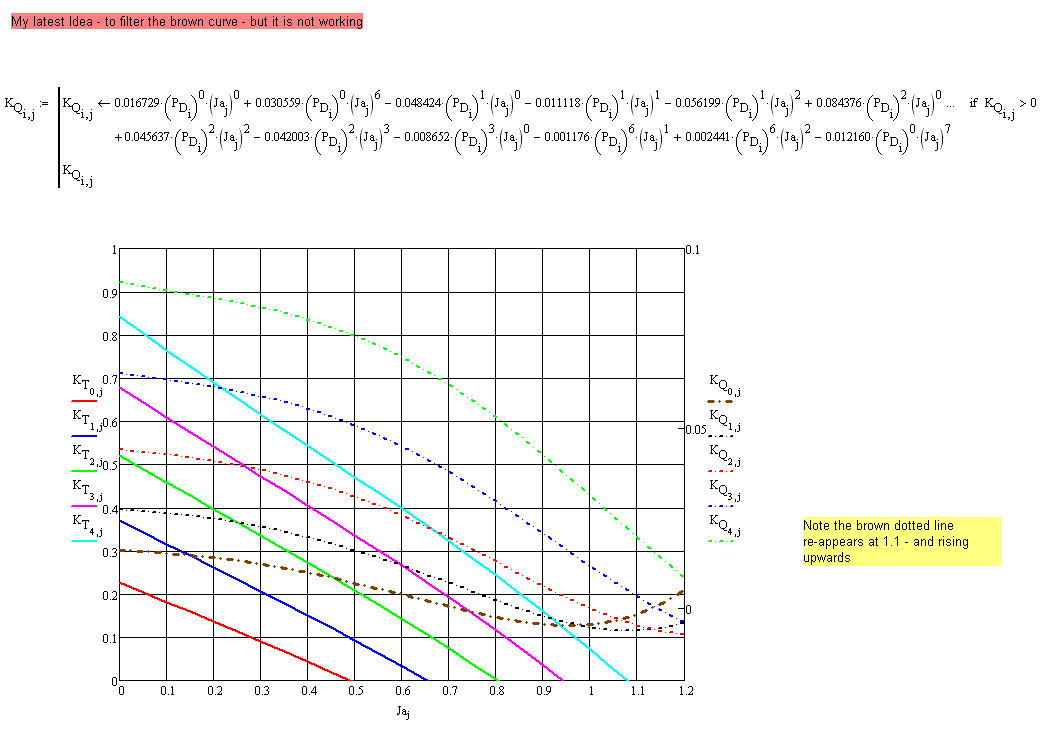
Many thanks for looking into this - and your proposal. I have been having some further thoughts about this - and have partly been able to answer my own question - but not completely.
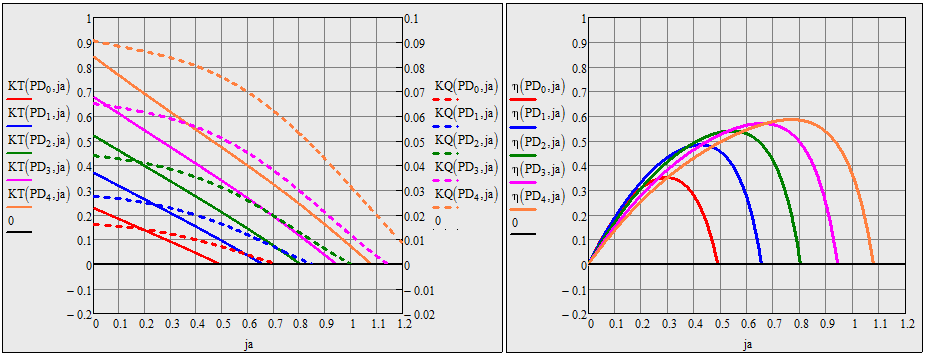
I have attached some pictures - and as you will see I have succeeded in filtering the rubbish out of the efficiency curves - but I have not succeeded in filtering the rubbish out of the Kt, Kq graph - in particular - the brown curve - which dips below zero - and then starts to climb up again.
Could I trouble you to explain why this is not working?
Look forward to your thoughts.
Gordon.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The new plots seem to be from a differnt data set. As far as I see you successfully suppress negative values but positive value are unchanged. It seems that you don't ant to see positive values after the plot is going negative the first time. You routine would not do that because every data point is handled on its own without considering what happend before. Furthermore the routine for filtering K.Q is obviously done after K.Q was calculated the first time. So there is no need to calculate all values again. On contrary - in your try to filter for K.Q you already have K.Q calculated and what you do is: if K.Qij is postive, you calculate the value again (to no avail), other you leave it as is, This means that K.Q wouldn't change at all.
For eta this is different as you filter while eta is calculated the first time, so values, where K.q is negative are not calculated and stay at their default value 0.
There are two reasons why I had chosen to set the values we want to filter not to zero but to the first negative value found:
1) If i would set the first negative value to zero, the last segment (the connection of the last point with positive value to the next) would be slightly false.
2) Keeping all filtered values negative keeps them out of the way. If they were zero, you could see them at the bottom, especially if you chose to add symbols like dots to the plots.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner,
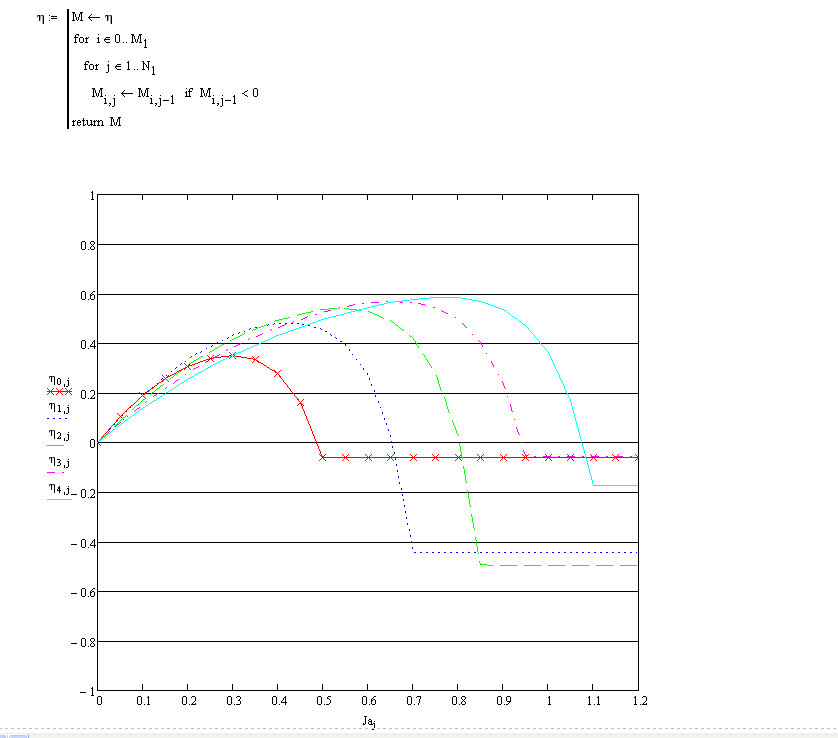
Many thanks for your help with this. I have had another look at your Mathcad spreadsheet - and have taken some screen captures - below. However, what I have done is change the "limits" on the Y axis - and secondary Y axis as you will see - to see what is happening at values below zero.
You are correct - I do want the graph plot to "stop" - when the Y value dips below zero - because in reality the Y value can't have a value below zero. However, what is puzzling me - is why can't the plot "stop" when the Y value dips below zero?
Looking at your graphs below - even with "rubbish" removed - the plot carrys on horizontally - when it really should stop.
Look forward to your thoughts on this.
Gordon.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
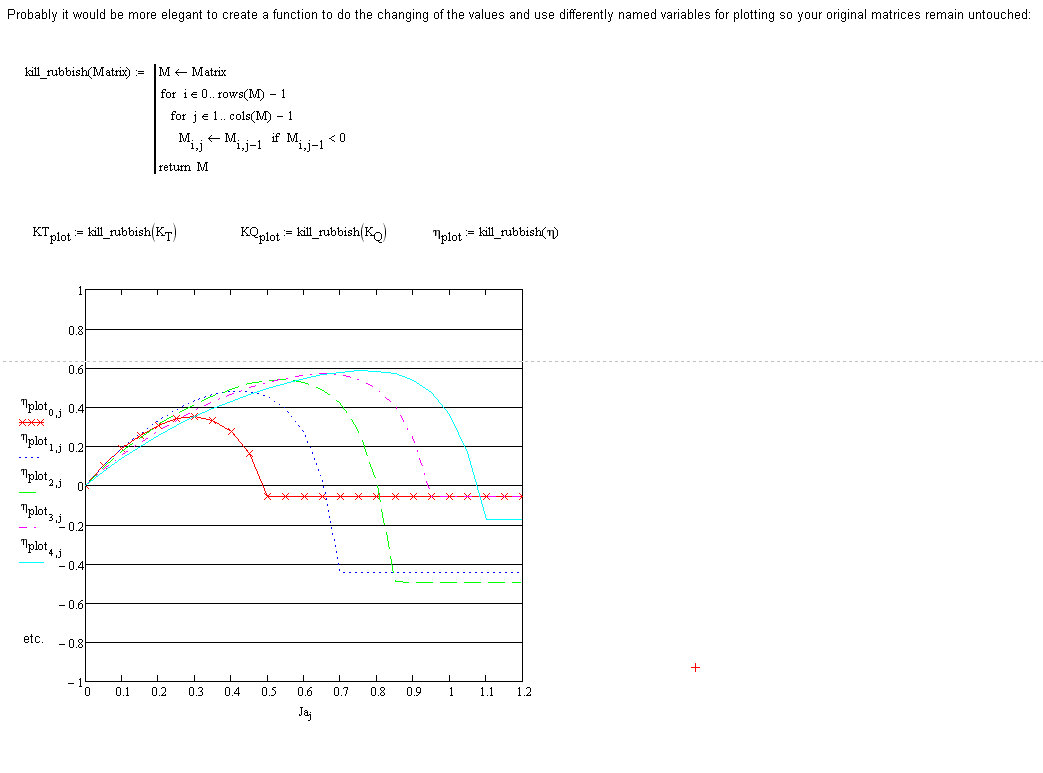
You never said that you would change the ordinate limit that way 😉
As explained above I was hiding the unwanted points below the abscissa. If you change the limit of course you will see them.
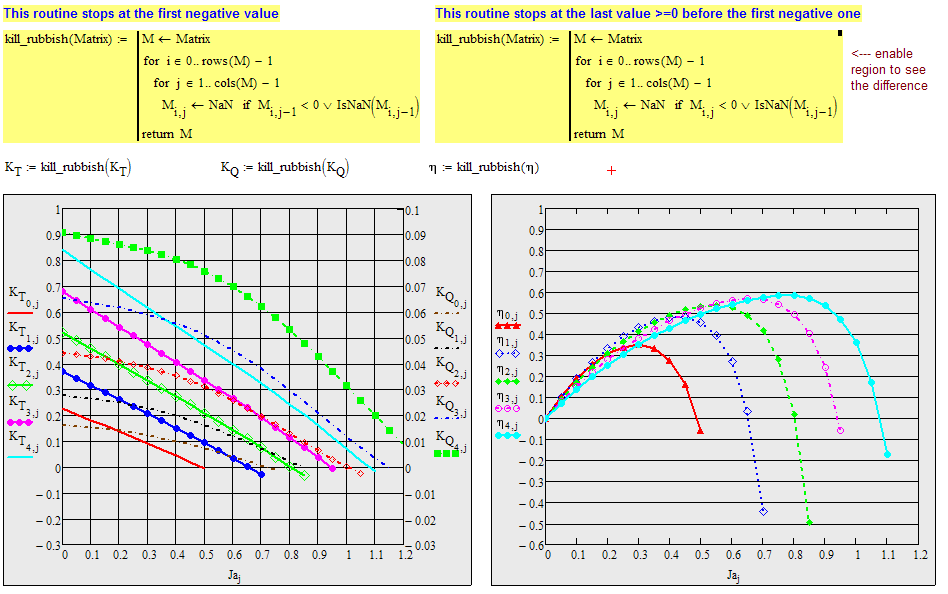
But as Fred had pointed out a more correct way to do it would be to assign those points a NaN (Not a Number) as "value". A 2D-plot would stop plotting at that special value.
Find below and attached two routines which do exactly that. The first would stop at the first point being negative (the plot will go more or less below zero that way) while the second stops at the last point still positive or zero (the plot stops above zero; similar to what Fred had achieved). So chose whatever you find appropriate.
The screenshot shows the result of the first routine.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you don't like my way of doing the filtering using programmed loops, you could use your range variables to do the same like this:
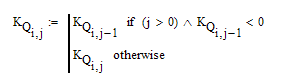
Nevertheless I'd prefer the programmed variant, especially using the function at the end of the sheet I posted.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you create KT and KQ as functions, then you can discard values that don't make sense to you. (Note that negative thrust and torque are both physically possible!)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
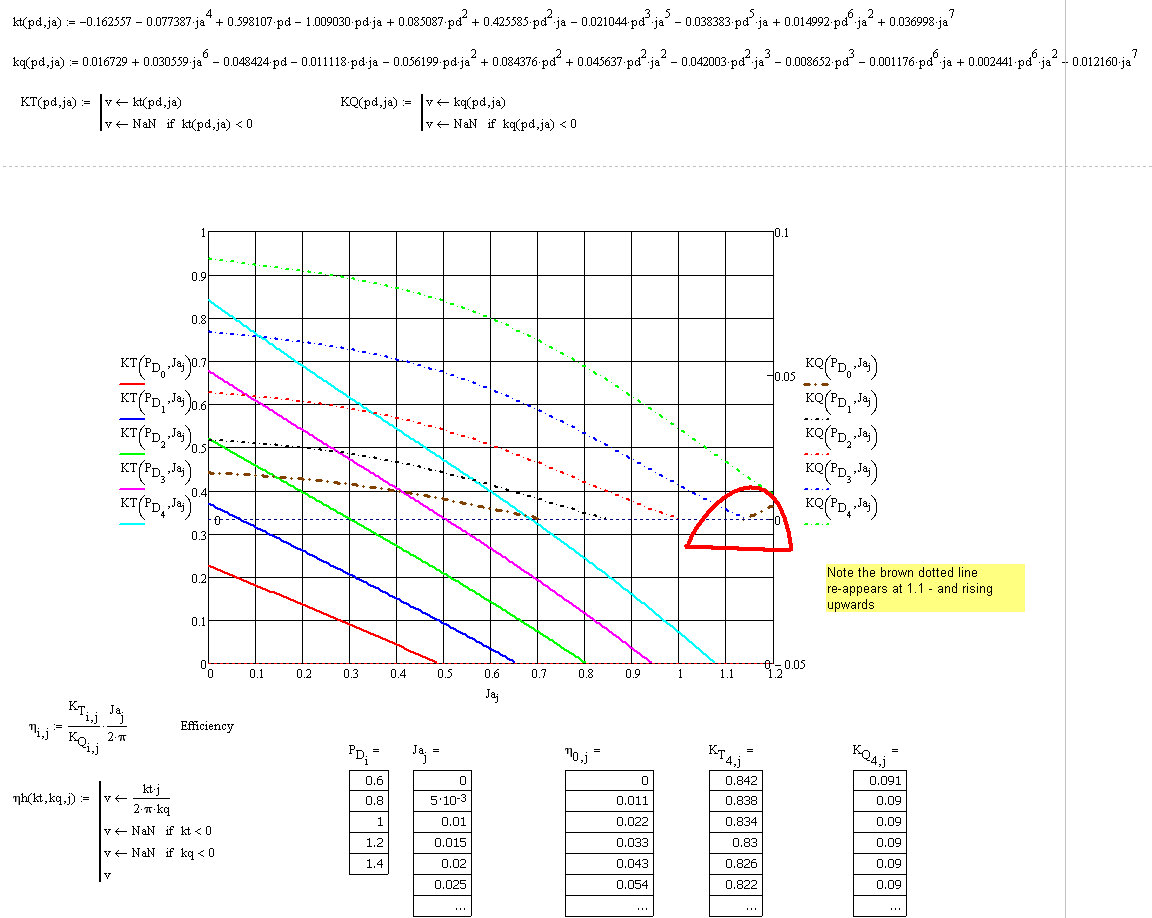
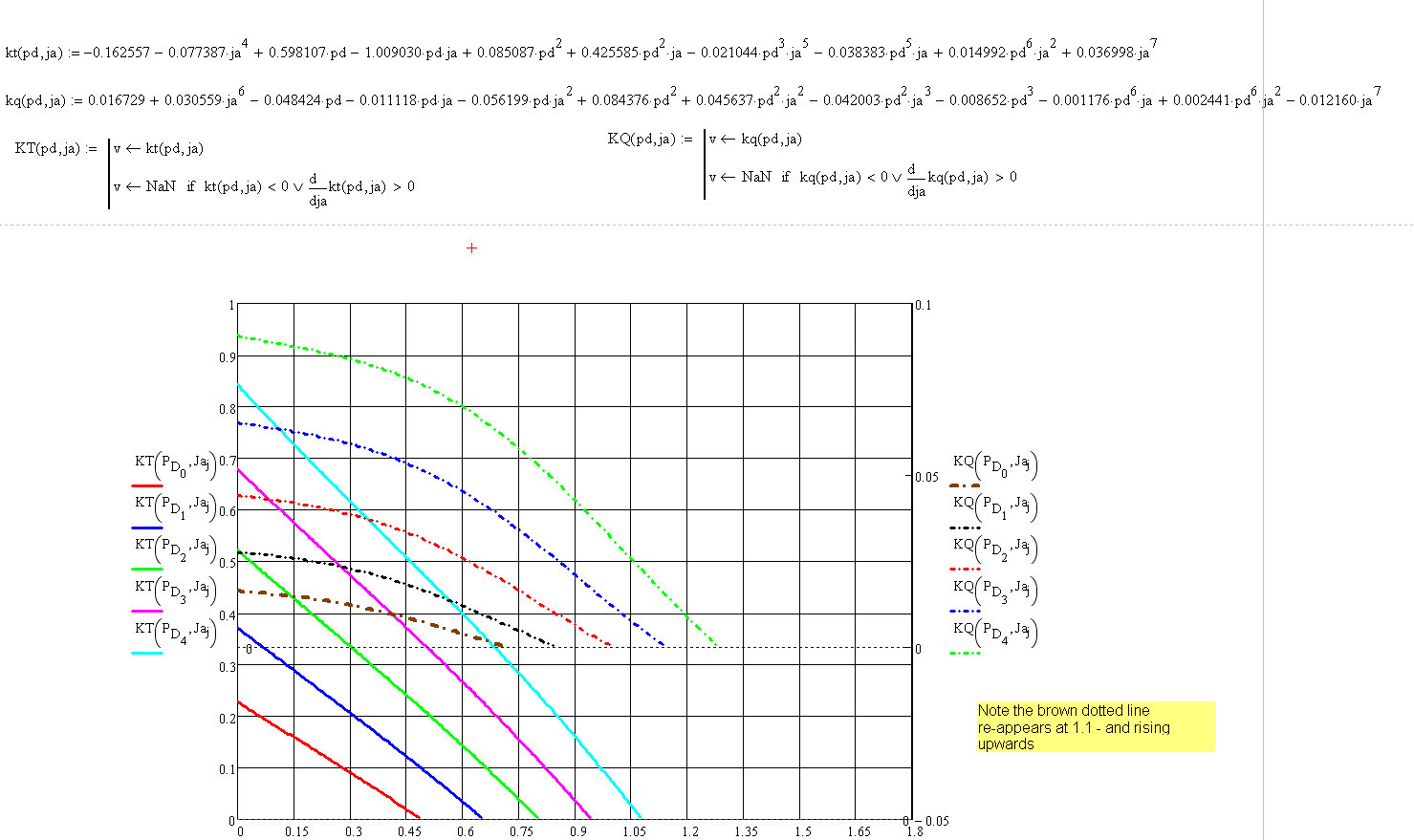
Hi Fred,
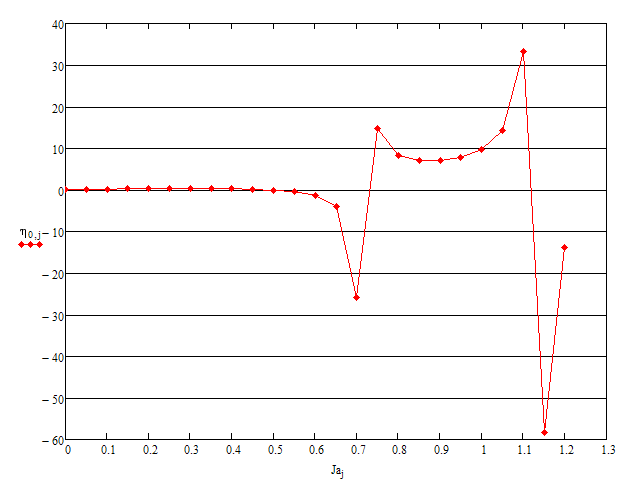
I much appreciate your help with this too. However, if you have a look at the first picture below - I have drawn a red loop - round a "small portion" of the brown dotted curve - which shouldn't be there. Any ideas why that is there?
I reduced the size of the "interval j" - and as you will see the efficiency curves look good - in the second picture.
So - the only remaining thing - is to sort the brown curve - which persists in re-appearing.
Look forward to your thoughts on this.
Gordon.
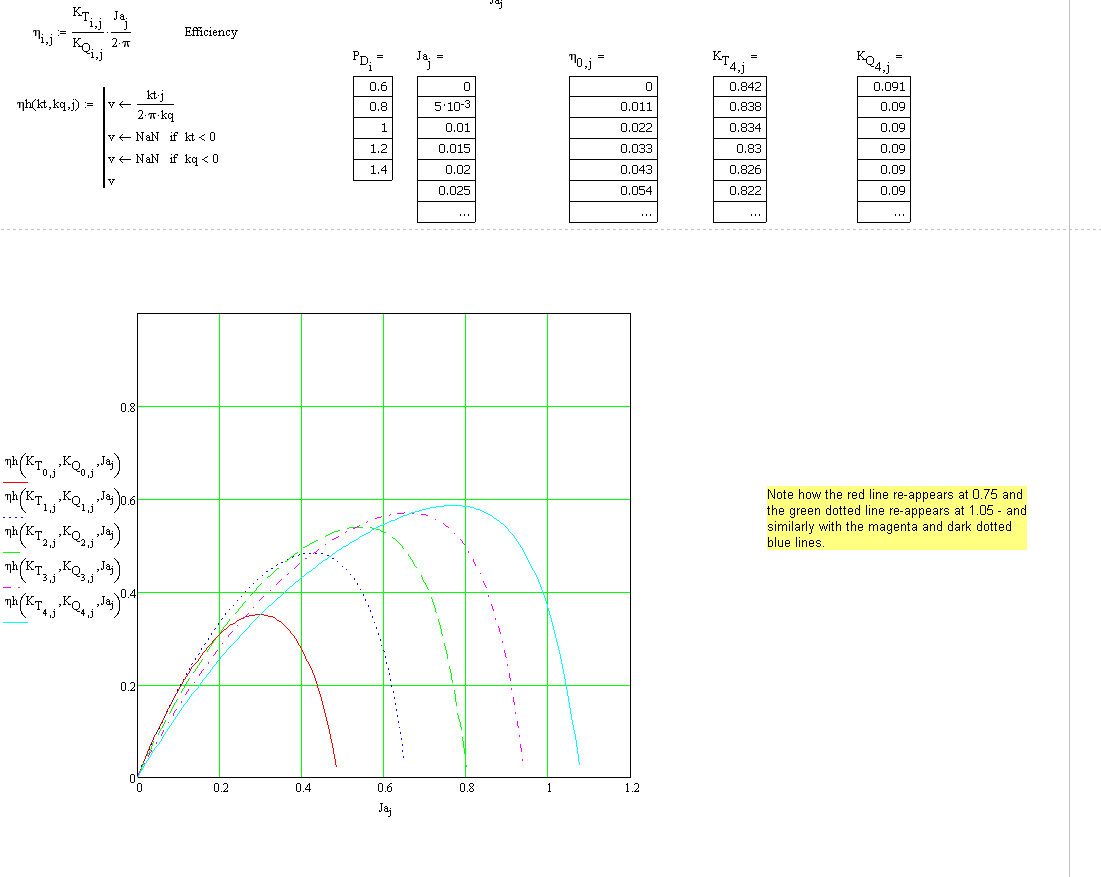
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred, Werner,
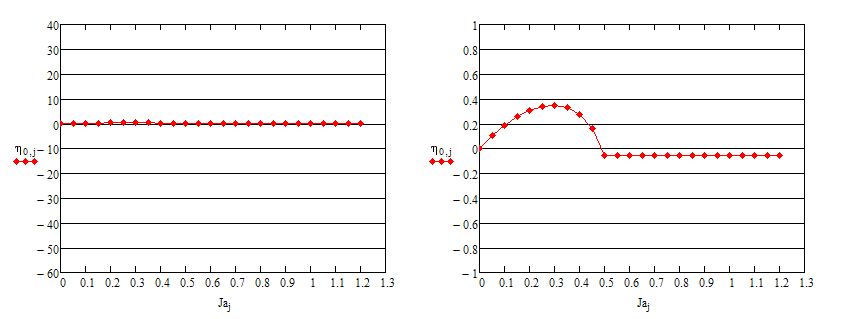
I deliberetly increased the X axis limits - to see what the polynominal curves were doing - once they had dipped below zero on the Y axis - and I noticed they all had positive gradients (first picture).
So I added the additional restraint of the differential of the curve - if it was positive - then it had to be a "not a number" as well.
I liked the idea of turning the regression equation into a function - that was a good idea Fred.
So I think this answers my question now - so many thanks to you both for your help. Much appreciated.
Gordon.
I 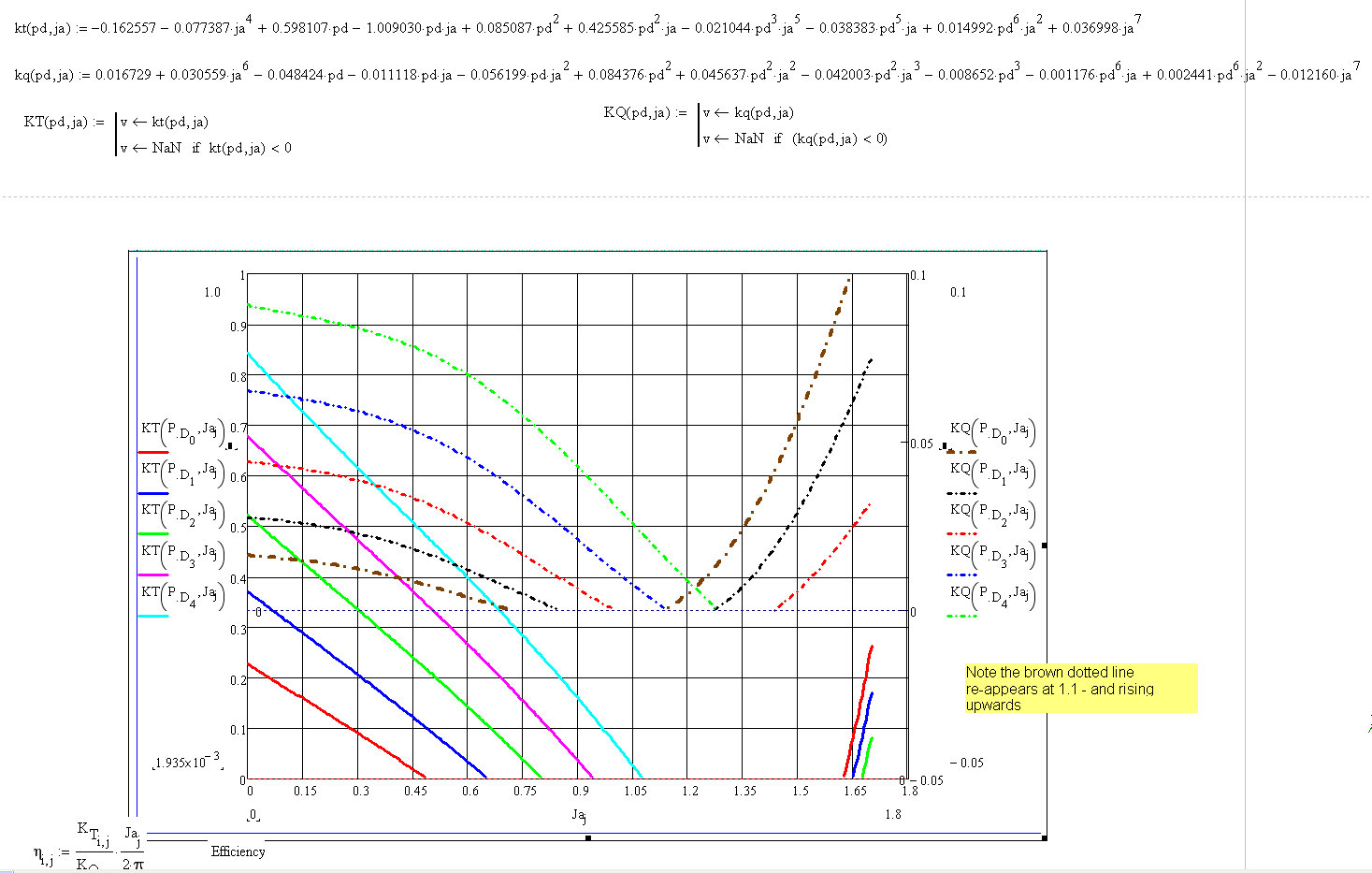
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Inspired by Fred - here is another functional approach. Plotting is somewhat slow as the functions will try to determine the zero point for every call to the function.
The local approach using the sign of the derivative sure is quicker and works, as long as the type of function doesn't change much. It will certainly not work for eta.But then my way of using root to find the zeropoint is also limited to "good behaved" functions KT and KQ.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner, Fred
I like your idea of finding the root of the function as it passes through the X axis - and then "effectively" terminating the function for any values beyond this point - which I think is a more "general" solution - that could be applied to a range of plotting issues - where you want to filter out the "rubbish" - that I had with a high order polynominal function - that is "erratic" - outside the range it was intended for.
I much appreciated the "team effort" from both of you - to solve this. Thanks.
Gordon.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- which I think is a more "general" solution - that could be applied to a range of plotting issues -
More general, but still fraught with flaws. Being slow is one of them, but even worse there are a lot of situations it would not work correctly all the time. Your functions eta for example. I have chosen finding the root of K.T_ (and not eta_) in eta(...) for good reason. Using root() we have not much control over which zero point would be found. It depends solely on the guess value which has to be constant in a general routine.
The usage of root(f(x),x,x1,x2), where we don't need to supply a guess value wouldbe nice, but it works only if the signs of f(x1) and f(x2) are different, as needed for a simple bisection. So the only way out I see would be to write a user routine similar to the aforementioned root without this limitation (stepping around in the interval until it finds a value x3 where f(x3) would have a different sign - primitive algorithm, but could work). This wouild slow down calculation time of the original function again significally.


