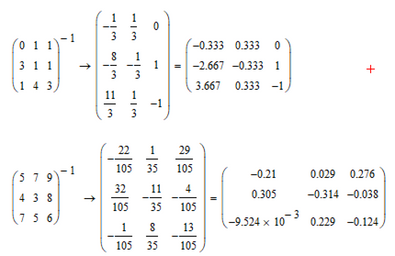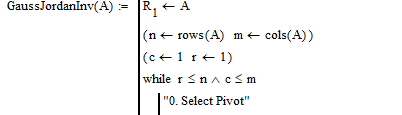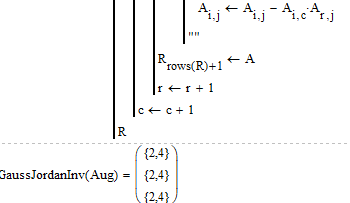Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Gauss-Jordan elimination method for inverse matrix
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Gauss-Jordan elimination method for inverse matrix
I try in Mathcad to build Gauss-Jordan method for obtaining the inverse matrix but it looks quite difficult.
It is closed to Jordan elimination method, but on the right side we consider initially (in the augmented matrix) an unit matrix. Did anyone build this method in Mathcad?
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cool ! I see that it makes also Pivotation. The problem is solved ! I attached the file.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may look up algorithms in "Numerical Recipes", I guess.
Writing an all purpose matrix-inverse-function and implementing it in Mathcad would require the knowledge of some "tricks" to make the algorithm as stable as possible, finding the appropriate pivot element, etc.
I am sure you can find a lot of references about this algorithm after a short internet research.
But what would be the benefit compared with Mathcads built-in algorithms, which usually are well tested, quite stable and much faster than anything implemented in Mathcads programming language?
You may be interested in this thread
https://community.ptc.com/t5/PTC-Mathcad/Gauss-Jordan-rref/td-p/273580
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
MAthcad fucntions are Black boxes. I want to apply just the numerical method Gauss-Jordan for the inverse of a matrix, a method that is open, transparent, and verifiable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@tubar wrote:
MAthcad fucntions are Black boxes. I want to apply just the numerical method Gauss-Jordan for the inverse of a matrix, a method that is open, transparent, and verifiable.
So for the start you sure would need some good advice about how to implement a stable algorithm.
Many algorithm implemented natively in Mathcad were based on the ones found in the above mentioned "Numerical Recipes" -> http://www.numerical.recipes
In Prime some were exchanged for the KNITRO tool box (with no advantage as far as I can tell).
Next step would be to implement the algorithm in C or the like and turn it into a user DLL which can be used from within Mathcad.
Then you may have functions which are fully verifyable and transparent which hopefully are as fast and reliable as Mathcad's built-in at the high price of a lot of work.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, are interesting the desires of PTC about Mathcad, but I remain faithful to the classical numerical methods implemented as they by the user itself.
The representation of the Mathcad's logical algorithm is very closed to the General Flowchart ( the logical scheme) of the algorithm of solving the problem, that's why I like it to use this way instead of Built-in functions.
I have the C++ and Matlab codes for "Gauss-Jordan elimination method for inverse matrix" and I want also to obtain a representation of it in Mathcad:
// Gauss-Jordan elimination for finding the inverse matrix
#include <iostream>
#include <vector>
using namespace std;
// Function to Print matrix.
void PrintMatrix(float ar[][20], int n, int m)
{
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cout << ar[i][j] << " ";
}
printf("\n");
}
return;
}
// Function to Print inverse matrix
void PrintInverse(float ar[][20], int n, int m)
{
for (int i = 0; i < n; i++) {
for (int j = n; j < m; j++) {
printf("%.3f ", ar[i][j]);
}
printf("\n");
}
return;
}
// Function to perform the inverse operation on the matrix.
void InverseOfMatrix(float matrix[][20], int order)
{
// Matrix Declaration.
float temp;
// PrintMatrix function to print the element
// of the matrix.
printf("=== Matrix ===\n");
PrintMatrix(matrix, order, order);
// Create the augmented matrix
// Add the identity matrix
// of order at the end of orignal matrix.
for (int i = 0; i < order; i++) {
for (int j = 0; j < 2 * order; j++) {
// Add '1' at the diagonal places of
// the matrix to create a identity matirx
if (j == (i + order))
matrix[i][j] = 1;
}
}
// Interchange the row of matrix,
// interchanging of row will start from the last row
for (int i = order - 1; i > 0; i--) {
if (matrix[i - 1][0] < matrix[i][0])
for (int j = 0; j < 2 * order; j++) {
// Swapping of the row, if above
// condition satisfied.
temp = matrix[i][j];
matrix[i][j] = matrix[i - 1][j];
matrix[i - 1][j] = temp;
}
}
// Print matrix after interchange operations.
printf("\n=== Augmented Matrix ===\n");
PrintMatrix(matrix, order, order * 2);
// Replace a row by sum of itself and a
// constant multiple of another row of the matrix
for (int i = 0; i < order; i++) {
for (int j = 0; j < 2 * order; j++) {
if (j != i) {
temp = matrix[j][i] / matrix[i][i];
for (int k = 0; k < 2 * order; k++) {
matrix[j][k] -= matrix[i][k] * temp;
}
}
}
}
// Multiply each row by a nonzero integer.
// Divide row element by the diagonal element
for (int i = 0; i < order; i++) {
temp = matrix[i][i];
for (int j = 0; j < 2 * order; j++) {
matrix[i][j] = matrix[i][j] / temp;
}
}
// print the resultant Inverse matrix.
printf("\n=== Inverse Matrix ===\n");
PrintInverse(matrix, order, 2 * order);
return;
}
// Driver code
int main()
{
int order;
// Order of the matrix
// The matrix must be a square a matrix
order = 3;
float matrix[20][20] = { { 5, 7, 9 },
{ 4, 3, 8 },
{ 7, 5, 6 },
{ 0 } };
// Get the inverse of matrix
InverseOfMatrix(matrix, order);
return 0;
}
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you use real Mathcad (not Prime but Mathcad 15) then you find information on how to write Mathcad DLLs if you go to "Help" and chose "Developer's Reference" .
Since I have little interest in Prime I am not sure where you could find the appropriate information for this version.
As far as I recall there are some threads in this forum dealing with DLLs for Prime.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I dont care DLLs. I just want to build a Mathcad algorithm for Gauss-Jordan elimination method to obtain the inverse matrix.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@tubar wrote:
I dont care DLLs. I just want to build a Mathcad algorithm for Gauss-Jordan elimination method to obtain the inverse matrix.
Oh, I see. So you don't trust Mathcad's built-in algorithms but you trust Mathcad's built-in programming language, which is a black box, too 😉
Implementing such a basic algorithm in a slow, interpreted language, as the Mathcad programming language at worksheet level is, is IMHO maybe a good exercise for students to do but nothing you would use for real, I guess.
Anyway - just go ahead and give it a try. If you get stuck you may come back and post your worksheet here to get help.
Maybe the link to the forum thread I posted above can be helpful (even though the matrix is only brought to echelon form there.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I want to build the Algorithm in the Mathcad interface. Already, in this Forum are presented some Jordan elimination algorithms (applied to obtain the solution) but this time I want to find the inverse matrix.
Unlike the other methods, the Gauss-Jordan elimination bring you to the exact/analytic solution (as you can see in the attached image file from the first message).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@tubar wrote:
I want to build the Algorithm in the Mathcad interface. Already, in this Forum are presented some Jordan elimination algorithms (applied to obtain the solution) but this time I want to find the inverse matrix.
Unlike the other methods, the Gauss-Jordan elimination bring you to the exact/analytic solution (as you can see in the attached image file from the first message).
Not sure what you mean by "exact/analytic".
Does Mathcads symbolics not qualify for "exact" and "analytic" in your eyes?
And the C-program you posted is only providing a numeric solution, not a symbolic, "exact" one. So whats the benefit?
But of course you are free to give it a try and come back for help with programming in Mathcad, if needed.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The Symbolic calculation tool is magnificent, but this time I want to apply the numerical method Gauss-Jordan for the obtain of inverse matrix.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@tubar wrote:
The Symbolic calculation tool is magnificent, but this time I want to apply the numerical method Gauss-Jordan for the obtain of inverse matrix.
Wow, thats confusing! First you wrote that the benefit of writing the Gauß-Jordan yourself would be the "exact/analytic" solution and after pointing you to Mathcads symbolics you say that you want a numerical solution.
I was eager finding out WHY you wanted to implement the algorithm yourself but I have to admit that I failed in finding out. Knowing your reasons could have helped finding an appropriate solution for your needs.
But, alas, I don't care about anymore. I just wonder why you don't go a head and give programming in Mathcad a try. It should not be difficult to implement the C program you obviously copied from
https://www.geeksforgeeks.org/finding-inverse-of-a-matrix-using-gauss-jordan-method/
in Mathcads language.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I try to avoid to many words for a clear problem. Thank you for the implication, but I wait from somebody with a concrete solution. I remember you helped me in the past, but this time maybe other persons will have a concrete idea on this defined problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You want it more like this?
Or is it this (the inverse of each of the matrices):
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nope, because of a long and barren talking now the people do not understand the Subject.
It is about the numerical method "Gauss-Jordan elimination" for obtain the Inverse Matrix.
Just closed with what is in the following links:
https://community.ptc.com/t5/PTC-Mathcad/Gauss-Jordan-rref/m-p/273580
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@tubar wrote:
Nope, because of a long and barren talking now the people do not understand the Subject.
It is about the numerical method "Gauss-Jordan elimination" for obtain the Inverse Matrix.
Just closed with what is in the following links:
https://community.ptc.com/t5/PTC-Mathcad/Gauss-Jordan-rref/m-p/273580
Close? The reason I pointed you at this thread was because Alvaro implemented there exactly what you had asked for! His RREF uses Gauß-Jordan and not only gives you the inverse of a square matrix but returns additionally the determinant and the rank. If you don't like the latter, just ignore it and pick the inverse only.
You may do this by using his RREF routine as it is
or modify his program slightly to just return the inverse matrix.
The "long and barren talking" is a result of your refusal to clearly state what your goal is. There is not only one Gauß-Jordan algorithm, if you look in the literature, but a lot of variants - especially the way to find an optimal pivot element (not always the one with the largest absolute value is the best). It depends upon your need and the numbers in your matrix which flavor of the algorithm will be best suited. But unfortunately you refused to reveal your real needs and talked about needing "exact/analytical" results in one post and about numerical ones in the next. You never commented on the link to Alavaros function which I posted in my first reply, never told us why this routine is not exactly what you are looking for. You just posted the link again in your answer to Luc.
And worst of all you never showed what you had tried and where you got stuck in implementing the algorithm.
I am sorry to have to say this, but you really created the impression of just being a student trying to talk others into making his homework.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I give you an example how I want to be builtthe algorithm. Just like the simple Gauss elimination method attached at this message. It is taken from L. Fausett - Numerical Methods Using Mathcad . Now I am clear, I hope.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, but where is is the point you have troubles implementing the algorithm? What have you yourself tried so far? Maybe we can help you with your efforts.
And whats wrong with Alvaro's RREF?
Alvaros routine does exactly what you want.
Just augment the unity matrix at the begin of the program and at the end return only the last part of matrix A (using submatrix). All this very similar to what I had shown in the picture above in the extern routine "INVERSE".
You may delete all references to d and rho as they are not needed to calculate just the inverse with Gauß-Jordan.
Be aware that Alvaro's program is assuming ORIGIN=1.
Be further aware that any error handling is missing, so you will even get a (wrong) result if the matrix is not invertible at al (if it does not have full rank).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I want Mathcad to perform iterations - as per the mathematical method. 99 % of users know that operation inverse(M). I know well the Symbolic tool its not necessary for me in this case, i want to get the inverse matrix mathematically.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It looks to me like you did not understand what Alvaro had written and not what I had done with his routine creating the INVERSE function.
You may want to have a further look at his sheet.
The symbolic evaluation was chosen to show you that you really get the correct result with the iteration compared to Mathcads built-in inverse
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I dont need operators like Gausselim or Inverse. Just a mathematical algorithm using logical operators to obtain the Inverse matrix trough Gauss-Jordan elimination.
If it is used any operator, it should be shown directly in the Mathcad's interface like GaussJordan(M)
I try to avoid discussions that divert my initially intended subject: ""Gauss-Jordan elimination method for inverse matrix""
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@tubar wrote:
I dont need operators like Gausselim or Inverse.
No idea what you are talking about. But if you are unable to open Alvaro's sheet and make the two already mentioned minor changes to get what you demand, I can't help any further.
Good luck and I hope you'll find what you are looking for (as you obviously don't realize that you already found it).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
His sheet is this one that use only Symbolic operators.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@tubar wrote:
His sheet is this one that use only Symbolic operators.
NO!
You are referring to Luc's sheet. He is using Mathcad 11 and the symbolic commands he is using are not availabe in Mathcad 15 anyway.
I was talking all the time of Alvaro's sheet. Its in the very first post in the old thread I linked at in my very first answer! And I also showed you in the picture in my post here
how you could use his RREF routine to get just the inverse matrix. Didn't you read that?
And later
I explained the few changes you'd had to apply to Alvaro's RREF function to make it just return the inverse matrix. Of course this routine would not be as stable as Mathcad's built-in and as also expained above will return a wrong result instead of an error if the matrix is singular - at least unless you add an error check (e.g. see if the rank is maximal).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I will check more what he wants to do on that file. It looks he wanted to obtain the determinant or the echelon form.
OK. We will see.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@tubar wrote:
I will check more what he wants to do on that file. It looks he wanted to obtain the determinant or the echelon form.
OK. We will see.
Yes, sure. His routine does more than you demand for. It returns the echelon form, the determinant and the rank!
And if you augment the unity matrix after the matrix and feed the routine with it, the echelon form would mean that the second half of the matrix is the inverse you are looking for!
Here are all the changes that have to be done to get a routine which returns the inverse.
But keep in mind that no error checking is done and so you get a (wrong) result in case the rank is smaller than the row number and the matrix is not invertible though. Furthermore Alvaro's sheet assumes ORIGIN=1. If you want to use his routine in a sheet with ORIGIN set to another value, you have to make changes here and there.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I studied more that file of Alvaro. In fact RREF( ) is an operator of Mathcad. I modified the file of Alvaro (I attached it here) and now I obtain the INVERSE through Gauss-Jordan Method.
It remains a problem: how I can vectorize the problem in order to get all the steps (intermediary forms) of the inversion process.
I dont ant just only the final form of the INVERSE, but also the forms for each step i=1...n.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Something like this?
In case you need more intermediate steps and you really mean the i-loop, you would have to move the highlighted line as indicated in the picture to get this result:
Upon further thinking about it I guess it would make more sense to move the line one up into the if-condition (replacing the "" now there). This should avoid duplicates. In case of your example there is no difference to the first variant, but with larger matrices you should get more steps that way. Think of that line (R[rows(R)+1 <-- A) as a way to make a photo of the condition of the matrix at the moment. Throw it in wherever you find appropriate. You may use this line multiple times, too, if needed.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, something like that, but for me doesn't work. For me it shows something like{2,4}...etc.
.........
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Select the result (the one containing the {2,4}'s), and from the menu Format=>Result, then "Display options" tick "Expand nested arrays".
Success!
Luc