Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Hare and Snell's law
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hare and Snell's law
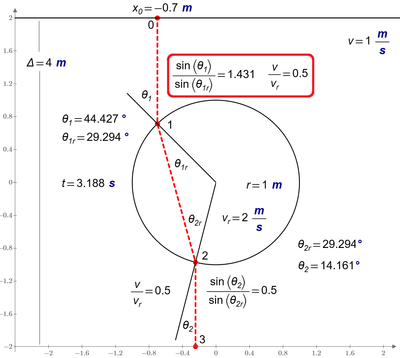
A hare from point 0 needs to cross a field with a length Δ and with two parallel straight edges as quickly as possible. The hare runs in a straight line perpendicular to the starting edge of the field and comes across the edge of a round section (point 1) where the hare can run faster (this round section of radius r is in the middle of the field). The hare changes direction of running, crosses a round section along a chord, runs out of it with a change of direction (point 2) and finishes along the shortest path (point 3). Determine the hare's running trajectory.
Why is the Snell's law fulfilled at point 2, but not at point 1? Where is my mistake or misunderstanding of physics (Fermat's principle)? See please the picture and the Prime 6 sheet in attach.
See too
The problem of cockroach races - PTC Community
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
-
Physics
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't think there is any mistake in Valery's reasoning. Rather, as he describes the problem, "The hare runs in a straight line perpendicular to the starting edge of the field and comes across the edge of a round section (point 1)." As given, point 1 is not a point to be determined by optimization, but a fixed point determined by the starting point and a perpendicular line. As such, any approach to the circle ending up at point 1 will have the same remaining optimal path that goes through point 2. There is no reason that Snell's law should apply at point 1 since point 1 is fixed and the incident angle theta 1 depends only on the defined approach.
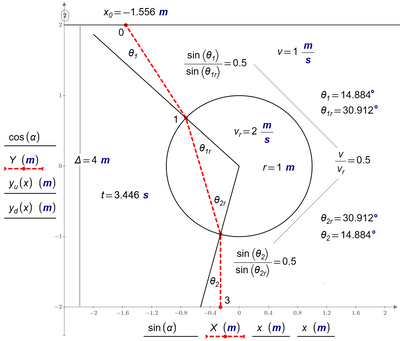
Werner solved a different problem where the path leaving the starting line is not constrained to be a perpendicular. Now, both points 1 and 2 are part of the optimization, and Snell's law will be satisfied at both points.
I think both are right - just that each addressed distinct problems.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The mistake of reasoning consists in the fact that the fastest way does not run from point 0 vertically down to Point 1!
If you take that into account, you no longer come into conflict with Snell and Fermat 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Werner!
You problem is another problem - this The problem of cockroach races - PTC Community
My task is this.
A parallel beam of light is incident on a flat plate perpendicular to the upper surface. Some rays of the beam pass in a straight line through the plate, while others rest against a spherical surface - they are reflected and refracted. A single ray of light does not know that there will be an obstacle ahead! How will a single ray of light behave?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
We have one photon (stupid hare) or a stream of photons (light of life - smart hare).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
How will a single ray of light behave?
The reflected part should be obvious and the refracted part of the beam will behave according to Snellius. It will land at the bottom line at some point 3. It will not be the fastest path from point 0 to the bottom line, though and also not the fastest path from Point 1 to the bottom line!
Fermat will work but only if you specify starting and end point but not if you want to specify the starting direction or if you just specify a line where the beam should end up.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't think there is any mistake in Valery's reasoning. Rather, as he describes the problem, "The hare runs in a straight line perpendicular to the starting edge of the field and comes across the edge of a round section (point 1)." As given, point 1 is not a point to be determined by optimization, but a fixed point determined by the starting point and a perpendicular line. As such, any approach to the circle ending up at point 1 will have the same remaining optimal path that goes through point 2. There is no reason that Snell's law should apply at point 1 since point 1 is fixed and the incident angle theta 1 depends only on the defined approach.
Werner solved a different problem where the path leaving the starting line is not constrained to be a perpendicular. Now, both points 1 and 2 are part of the optimization, and Snell's law will be satisfied at both points.
I think both are right - just that each addressed distinct problems.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, different propblems.
And Valery specified in in his last response a third problem, too, which seems to be the problem he is really interested in.
namely, what the path of a beam of light sent vertically down and meets the circular disk of different density.
The answer is - just use snellius and forget about it being a minimization problem using Fermats principle. Fermat is about a beam where both the starting and the endpoint are given. In case of Valerys problem, the endpoint is not given but determined by Snellius law.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
An old Jewish joke.
Two students come to the professor and ask him to solve their dispute - how a hare runs across a field with a circle inside. One student says that it is so, another that it is different.
The professor says they are both right.
But then the professor's wife shouts from the kitchen: "the students cannot be both right at the same time!".
The professor says that you, wife, are also right.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A photon of light (hare) falls perpendicularly onto a flat glass surface (runs out onto the field).
How does a photon (hare) need to know that it needs to fly no further straight, but turn to the side, refracting its run?
To be, or not to be. that is the qustion!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
New old task - v > vr.