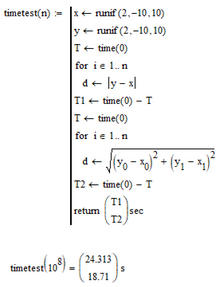Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to traverse a curve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to traverse a curve
Dear all,
I have a set of close points (every 20 mm for a 100m long curve) which I can import into Mathcad and use linterp to create a temporary function.
But when I need to call the function, I need the input to be the length of the curve. For example,
If I have a function y = sin(x) and I need to have a function which calculates the slope (tangent) at a distance 'd' but the distance is measured along the length of the curve sin(x) and not at x=d..
Is there any straightforward way of doing this ? I can think of one crude way (slowly start traversing the curve in small increments of x and keep on adding distance between y(x) and y(x+dx) until 'd' is reached and thereby now we know the (x,y) coordinates for the function and go from there). But I have to use this routine thousands of times and I don't think my method is efficient at all.
Please suggest ?
Warm Regards,
Aravind.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you already turned your points into a function (via linterp, splines, or whatever) you may use the integral formula for curve length to do the job.
You are best off if you post a worksheet with your data and your attempts and maybe some concrete numerical examples to show what exactly you are looking for.
As far as I understand you try to derive a parameter representation of a function with curve length as parameter, when a cartesian representation is given.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you already turned your points into a function (via linterp, splines, or whatever) you may use the integral formula for curve length to do the job.
You are best off if you post a worksheet with your data and your attempts and maybe some concrete numerical examples to show what exactly you are looking for.
As far as I understand you try to derive a parameter representation of a function with curve length as parameter, when a cartesian representation is given.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Awesome ! I didn't know that there is a simple integral which gives length of curve 🙂 (1 + (dy/dx)^2)^0.5
This would work perfectly, except I need to use it in reverse (I know the length and I need to find the x). I think since it's just one equation+variable, given+find block should be fast enough to use in a loop.
Thanks a lot Werner !
Sorry for not giving any data (Actually I am yet to start making the sheet and was brainstorming ideas on how to achieve my goal and I thought my solution was just too bad so decided to ask for help right away )
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes , a solve block would give you the inverse you need.
Something like this:
Depending on the function you use I guess its better not to use a constant guess value but rather make the guess for x dependent on the curve length in some way as shown in the file. But that depends on the function you have. You may give it a try with a constant guess at first.
Mathcad 15 sheet attached.
EDIT: One additional remark. As you are looking for the derivatives I think you should not use linear interpolation but rather spline interpolation for smooth results.
If you stay with linear interpolation, then determining the x-value from a given "curve" length could be programmed easier and exact as it would just mean to determine the length of line segments or parts of them.
Furthermore the "derivative" would be constant between two of your points and not defined at the points themselves (or you may calculate the mean value for them).
BTW, the time consuming part in my approach is not the solve block but rather the numeric derivation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot Werner !
The reason why I use input data as close as possible (20 mm interval for a 100m cable for example), and use linterp is that although it is approx, the slopes are almost correct (I dont use derivative but I use (y2-y1)/(x2-x1) for two points on either side of the given point).
I heard that using splines sometimes creates an issue (it sometimes makes ripples between the points (as shown in red) instead of joining them in the sketch below). Since I have closely spaced points in a large cable length, there is no way I can spot these in a graph, but this will grossly affect my results because my results are very sensitive to the calculated slope.
(please pardon the rough sketch)
Am I thinking wrong ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner,
Could you please tell me why the attached sheet is not working ?
The solve block is able to find a solution on either sides of a point but is not able to find the solution at that particular point (although it is just part of a straight line since I used linterp function).
Your help is much appreciated !
Aravind
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A "simple" problem of numerical precision of the integration.
If you decrease TOL to 10^-4 (from the default 10^-3) the problem is solved (at least for this specific input value).
Unfortunately decreasing the values of TOL and CTOL increase the calculation time for the numeric integration.
So if you want to stick to linear interpolation I'd prefer a simpler and more exact solution to get the result by using the fact that we are just dealing with line segments.
But would it make sense to ask for the derivative if you use linear interpolation? It would be constant between two points and what should the derivative be defined at the points where the line segments join?
And why do you think that the value corresponds exactly to one of your points? It doesn't.
The last point corresponds to an input value of approx. 85.100 and the last but one to 19.999.
So all three values corresponds to points somewhere in-midst the last line segment.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I agree.
Could you please give me a hint on how to find the solution faster (instead of using solve block on a finite integral) ? My input curve could be anything (straight line / circular / spline) so I decided to just break them up into a thousand parts and connect them with straight lines.
This way one approach would work for all types of input (straight lines / circles have equations but for splines I only get a set of points defining the curve).
I don't use differentiation to find the slope at any point (like you said, the linterp function is not differentiable at the points where lines meet). Instead I used the old method (f(x+0.001)-f(x-0.001) / 0.002) and I found results to be okay(ish).
I do face the problem of the sheet running for a whole lot (15 mins or more !) before it can accomplish the purpose and I would really appreciate if you kindly took a glance at it and suggested improvements. The sheet is attached (comments in yellow )
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you can break your input file into small line segments, the attached approach should be quite faster.
Couldn't test is with your new file as the data file (Excel) was missing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah sorry.
It is the same data as the one you used. I was trying out different input ways for it and I forgot to input back the coordinates.
It's embarrassing a bit but your solution was totally and completely greek and latin to me xD. Could you please explain it at layman's level or point to a source of information ? (In your segments(list) definition, I could understand that you transposed the list matrix, nothing else !)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, lets start:
"segments" is a function which takes a list of points (n x 2 matrix) and creates a vector consisting of the cumulated lengths of the various line segments with 0 as the first entry. This is achieved using Mathcads ability to work with vectors directly. Transposing the "list" matrix is necessary because MC15 does not offer a way to select a specific row of a matrix, we only have a column selector. Now I go throw the transposed list, chose two consecutive points (=columns) and let Mathcad calculate the distance between those points. The total length calculated so far (R[i-1) is added and the result is the next cumulated valued.
So the last value in the return vector is the lenght of the whole curve, the third value in the returned list is the length up to the third point, etc.
"absc2" (you should definitely use other names) calculates now the x-values for a given curve length "d" so it can be compared to the values of "absc" created using the integral and the solve block.
First I find the the largest value in the list "s" of cumulated segment lengths which is still smaller than d. So we know which segment we should have a close look to. In the next segment kind of reverse linear interpolation is used to find the delta_x value we have to add to the x-value of the end of the previous segment to get the value we are looking for. Basically just a matter of an equation of ratios.
"deriv" is working similar, but directly returns the derivative. This is easier to accomplish, as the derivative simply is the slope of the segment we found.
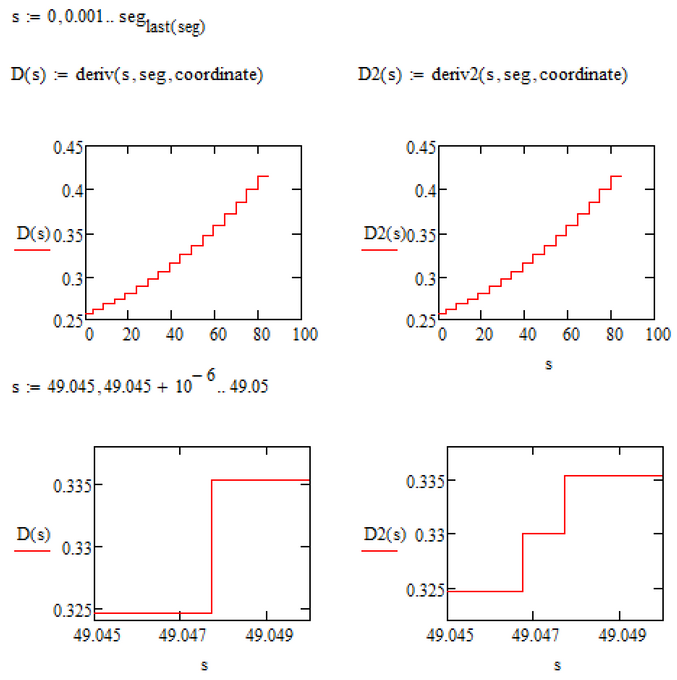
"deriv2" has the additional feature that for curve lengths values which lead in the area (10^-3) around a given point (excluding first and last point) the slope of the two line segments is averaged instead of returning just one of them.
The difference can hardly be seen unless you zoom in and you have to decide whether its worth the effort or not.
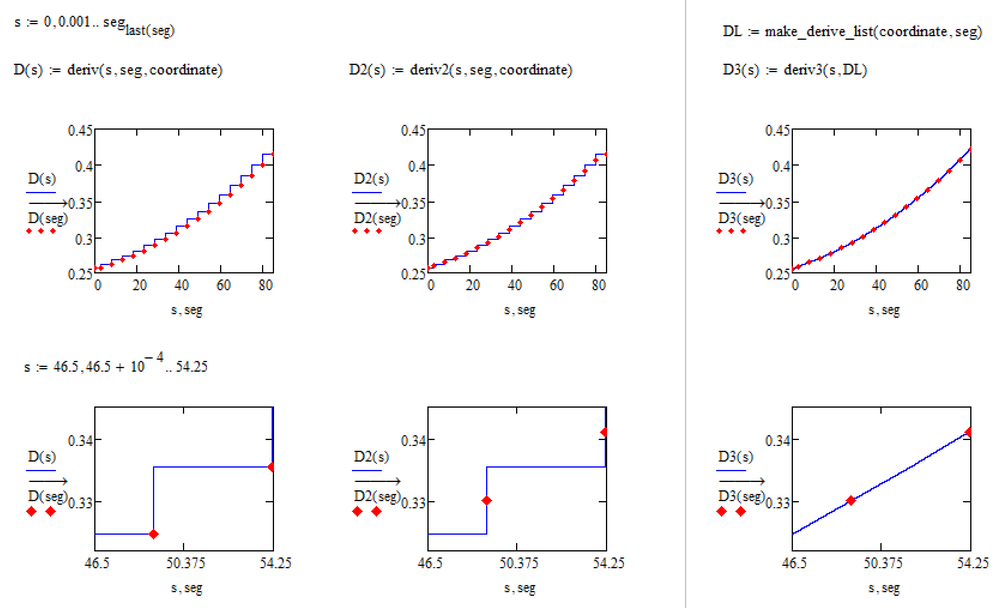
One additional idea: If its mandatory for the derivative to be smooth or at least stepless, I guess we could create a deriv3 where the result would be a weighted average of the two nearest slopes. Only if we are exactly in the center of a line segment, the slope of just this segment would be returned.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner,
Many thanks for the explanation ! But unfortunately I still didn't understand it XD
Could you please explain the first part of your code line by line ? For example
O <- ORIGIN
Is this an inbuilt command in mathcad ? What does it mean ?
Ro <- 0
Does this mean distance of first point from origin is 0 ? Why use O instead of 0 (zero) ?
for i belongs to .... why use O+1 instead of just 1 ?
The part where you calculated distances between the points using "vector algebra" is awesome ! I just realized |a| could also give the length of the vector (I thought it's only for absolute value of numbers). Is this method faster than the cartesian one (sqrt(x2-x1)^2 +(y2-y1)^2) ?
Sorry for the bother 🙂 I really hope you don't mind.
Warm Regards,
Aravind.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@adnn wrote:
Hi Werner,
Many thanks for the explanation ! But unfortunately I still didn't understand it XD
Could you please explain the first part of your code line by line ? For example
Unfortunately we cannot simply copy and paste picture in our posts here in this forum. It looks good when editing the post, but gets damaged when pressing the "Post" button. You must save the pic to a file and insert this file via the "Photos" icon - quite cumbersome, I know.
O <- ORIGINIs this an inbuilt command in mathcad ? What does it mean ?
ORIGIN is a system variable you can change either like a normal variable in the sheet or via the menu "->Tools->Worksheet Options->Built-In Variables".
By default numbering in vectors and matrices start by 0 and by changing the variable ORIGIN you may change this. Personally I prefer the default but some prefer to start the indexing at 1. When I write utiity functions most of the time I like to make them ORIGIN indepedent so they would work the same whatever the value of ORIGIN is.
But because ORIGIN is a 6-letter word I define a variable O in my programs and use this instead of ORIGIN (it also reminds me on 0(zero), the value I am used for ORIGIN).
Ro <- 0Does this mean distance of first point from origin is 0 ? Why use O instead of 0 (zero) ?
Yes, this creates a vector with just one element, 0. Its the fictive length of the non-existing "line segment" before the first one. In the absc2 function I use s[i-1 and if i=1 this refers to the element 0 in the segment list which hast to be present and has to be zero for the function to work.
The reason I use O instead of 0 is, as explained above, the attempt to make the function ORIGIN-independent. If you set the ORIGIN to a value different than 0 (lets say 1) the function will still work. If I hard code a zero as index, you would get an error if ORIGIN=1 because there is no index 0 in this case.
The same goes for O+1 and not just 1. It only matters if ORIGIN is not set to zero. O+1 denotes the second possible index.
If you use those functions in sheets with ORIGIN=0 only, you may delete all definitions of O and replace all occurrences of O by 0 without running into problems.
The part where you calculated distances between the points using "vector algebra" is awesome ! I just realized |a| could also give the length of the vector (I thought it's only for absolute value of numbers). Is this method faster than the cartesian one (sqrt(x2-x1)^2 +(y2-y1)^2) ?
Yes, |a| can mean absolute value of a scalar, absolute value of a vector or even the determinant of a square matrix. Especially in the latter case Mathcad often can not determine correctly what you mean and so you have the option to chose between "Absolute Value" and "Square Matrix Determinant" if you right click the absolute sign.
I used the absolute of vectors because its shorter and much more convenient. I had also expected this built-in command to be a bit faster than using squares and root. But as you asked I gave it a try and, alas, squares and roots are faster as you can see in the screenshot below - surprise!
BTW, in the meantime I added a third "deriv" function which works faster and gives a smooth result thanks to linear interpolation:
I gave the sheet you posted at last a try and copied the data from your trial sheet. It still is not working as of a couple of undefined variables.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot Werner !
Sorry I was away for the past few days. I applied the code which you gave earlier and viola, it solved my problem instantly !
I also used something similar to deriv2 (at points of kinks, I average the slope to the left and to the right) and I noticed that the error is negligible (in AutoCAD we have an error tolerance of 1mm usually, this was well within that).
For now, I think the code works perfectly 🙂 Thanks again !