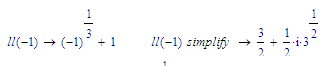Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Incorrect use of solve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Incorrect use of solve
Hi,
Distractedly, I used the "solve" operator to solve the given polynomial equation. It gives a solution but the answer is not complete. Why solve does not give the correct answer?
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
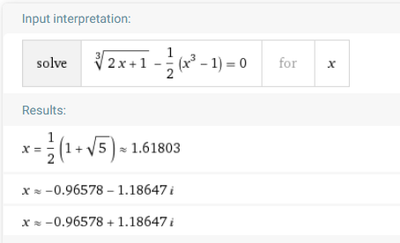
It's correct use, but potentially incorrect results, of solve.
Apparently the exponent 1/3 is problematic. When given "(2*x+1)^(1/3)-(x^3-1)/2, solve x",
this is what WolframAlpha makes of it:
Note that:
and
each give you all 9 roots, but:
Gives 7 roots, and 6 duplicates. maybe if you add ", all" to the solve command it comes up with more.
Finally, check if -1 is a solution:
Apparently not. This is the wonder world of the exponent function when it's argument is (potentially) complex.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's correct use, but potentially incorrect results, of solve.
Apparently the exponent 1/3 is problematic. When given "(2*x+1)^(1/3)-(x^3-1)/2, solve x",
this is what WolframAlpha makes of it:
Note that:
and
each give you all 9 roots, but:
Gives 7 roots, and 6 duplicates. maybe if you add ", all" to the solve command it comes up with more.
Finally, check if -1 is a solution:
Apparently not. This is the wonder world of the exponent function when it's argument is (potentially) complex.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the reply. Greetings.