Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Influence of TOL parameters on numerical integration
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Influence of TOL parameters on numerical integration
Hi everyone,
This is a question involving the functioning of the numerical integration operator in MathCAD 13.
In my worksheet I am solving a complex problem which involves numerical integration of multiple periodic functions.
While testing the solution, I am varying the parameter TOL between 10^-3 and 10^-15 to see which influence it has on the results. Now, one would think that, as TOL decreases, the solution should go to some sort of convergent point. But, as one can see in the attachment, the solution first is convergent, than starts to deviate and seems to go to a convergent solution again.
My suspision is that this is due to the internal integration algorithm of MathCAD13. Has anyone already seen this behaviour? Is it normal and can it be avoided?
thanks,
Ruben
P.S. Unfortunately, due to IP issues I am unable to post the worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting, never thought about that behaviour. Without the sheet we cannot test what the effect would be in newer versions of Mathcad, though.
There is a quicksheet (at least in MC15) dealing with the effects of TOL on definite integrals, also mentioning that decreasing TOL can make results less accurate.
"Solutions" given are chosing a different method of integration or breaking the integral in pieces in case of periodic functions.
I include a pdf made from that file for your reference.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the intel. Indeed, I also find it annoying that I am not able to send the worksheet.
Would anyone know if the integration algorithms have received a review in MathCad Prime?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I just gave it quick try with a rather simple integral, but a similar effect as in your pic can be seen for TOL=10^-5.
The results are the very same (including the outlier at 10^-5 and the rather big inaccuracy at the default 10^-3) in MC15 and in Prime2 (difference is that in Prime I only can show, copy and paste 15 decimal places).
I thought it would be possible to do it with a small program, but I neglected the fact, that the local assignment of a variable TOL would not influence the worksheet variable TOL.
So the only way seems to be manually changing TOL and copy and paste the result in a vector 😞
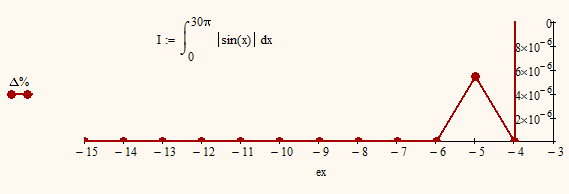
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yeah, I know, it took me an hour to make the plot I included first (my calculation algorithm is rather lengthy). It is nice to see that similar effects turn up with other functions.
Now, foolishly thinking I could be better than MathCAD I attempted to solve the issue with a homemade 'rough' integration algorithm which turned out to be as slow as a snail on a ramp. Hence, did not work out that well.
Also, I tried a Monte-Carlo simulation but, as this is a simulation, the error in the solution was too large when trading speed for accuracy compared to the MathCAD internal integrator.
Unless someone thinks of something else, I think I'll have to live with this.
thx for the help


