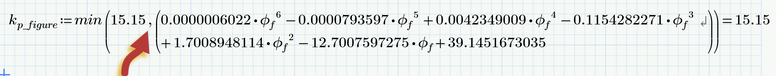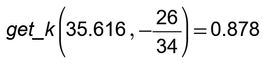Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Multiple Nested If Statements
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Multiple Nested If Statements
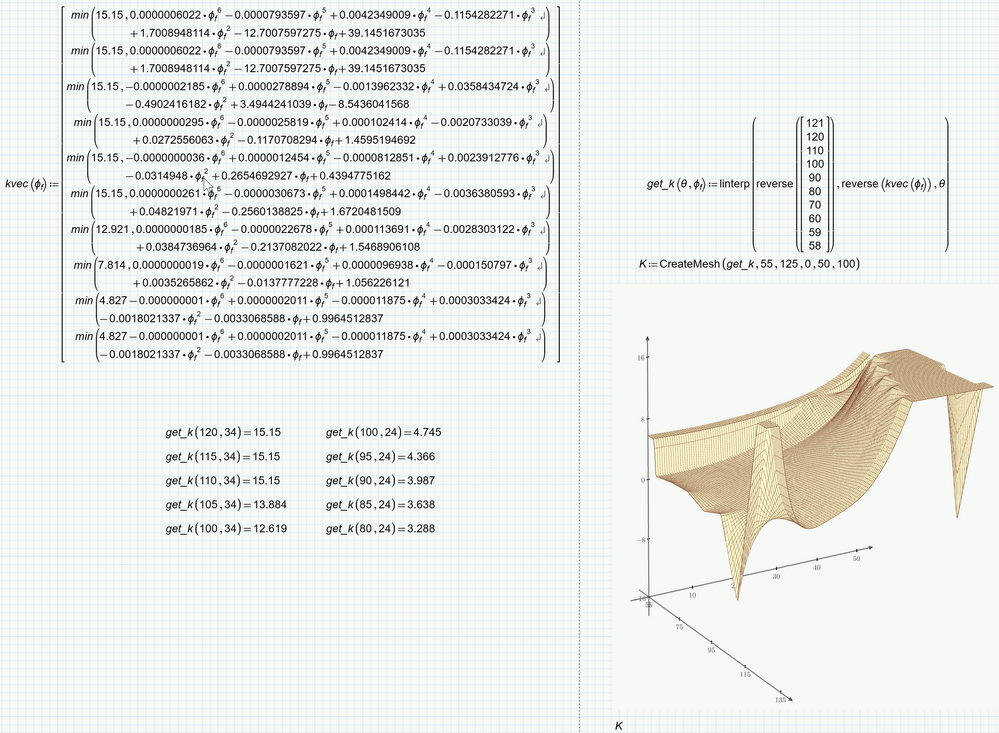
I would like to create a series of nested If statements to calculate kp_figure for Multiple values of Θ (120, 110. 100, 90, 80, 70, 60, and 50), with a secondary If statement for each value of Θ as shown in the calculation for Θ =120.
Any assistance would be appreciated.
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have an (implicit) multiplication dot between the 15.15 and the polynomial.
You have to separate the two arguments of the min function by a comma:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
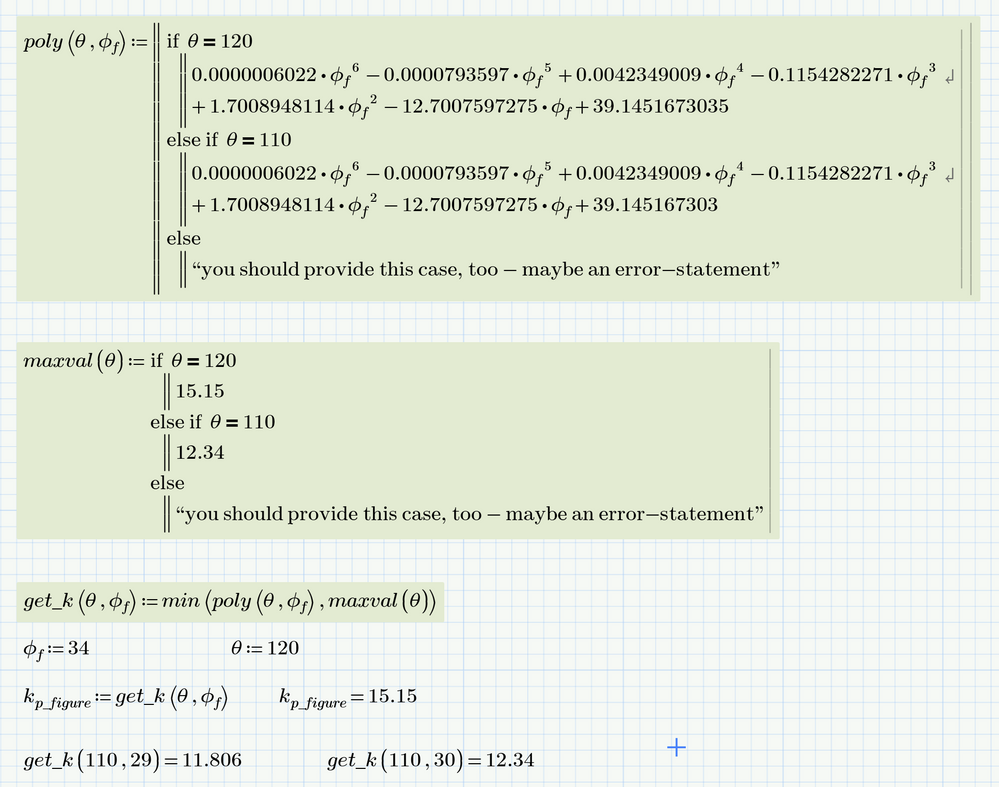
You don't need an if-statement to calculate the k value. After all its inefficient to calculate the polynomial twice. Let the min-function do the job:
How about defining some functions to do the job?
I was assuming that both, the polynomial and the max value are different dependent on theta. If thats not the case, the solution can be quite simpler. If for instance the polynomial is the very same for all values of theta (and only dependent on Phi.f, you won't need theta and the conditionals in the function "poly" and you also may consider providing the values for theta and the appropriate max-values in vectors and use "Lookup" to chose the correct value instead of the cascaded if's.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, the maximum value and polynomial are different for each value of theta. I am trying to develop a program/routine to calculate k when the values of theta and phi are changed/entered. I like the efficiency of the min function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have programmed the poly, maxval, and get functions, but have some undefined variables.
any ideas?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can't evaluate a function definition (unless its a constant function).
Delete the evaluation (= sign) and it should work OK
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Great. Thank you!
I have also tried using the min function, but it does not provide the correct answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
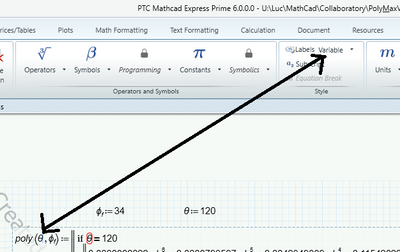
You've been hit by Prime's (in)famous 'autolabelling' feature.
The theta in the function declaration for the poly() function is labelled as a 'variable'.
All theta's appearing in the if statement conditions are 'automatic'.
That makes them different beasts, so Prime complains.
Make sure that all variables that should be the same variable, are labelled identically.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime's autolabelling often is a PITA and the cause of quite some unexplainable (on first sight) errors.
But this time, for once, this feature is blameless.
The combination of "Variable" and "(-)" works OK. Its usually a problem when used with symbolic evaluations.
Prime is simply complaining that it can't evaluate the function without knowing the value of theta. Thats OK, even though we wished for an error message more to the point (something like "numeric evaluation of function definition not possible").
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You're right, I missed the =
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It appears like this could be what you are after:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'll post this at the end of the replies also.
With the = deleted, the poly function works correctly. Thank you!
Now for the min function. Is this a mislabeling error?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have an (implicit) multiplication dot between the 15.15 and the polynomial.
You have to separate the two arguments of the min function by a comma:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much for your assistance! I appreciate it very much.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner already explained the error you made here.
What about values of theta other than 180, 170 etc.. What about, e.g. 175?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Luc for the information and help provided.
Intermediate values will require interpolation between the provided values of theta/
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
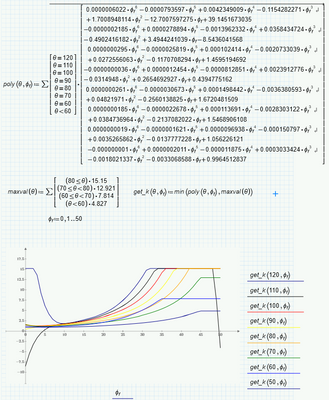
So I would suggest to include that interpolation in the function "get_k":
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner, Thank you for the help with the interpolation. That is a great help.
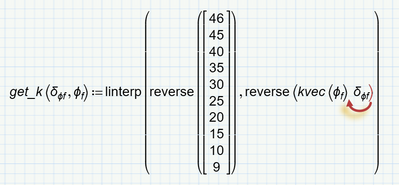
I have attempted to use the interpolation tools with some additional equations that are related to the first set, There is an error in the get_k function that says 3 arguments are required. Any ideas.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime is right - linterp requires 3 arguments and you provided only two.
Watch the closing parenthesis and the missing comma, to separate the third argument.
Furthermore I guess you meant to switch phi.f and delta .phi.f.
Furthermore you must move down the region a little but as otherwise it uses the definition of kvec from above.
Not sure if you really intend to get negative values but thats the way you defined your new kvec function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner, thank you very much for your assistance! It is greatly appreciated!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It has been awhile since I requested assistance with this worksheet. It got put on the back burner for a few months. I am still struggling to correct errors in the final calculation. Please see attached worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
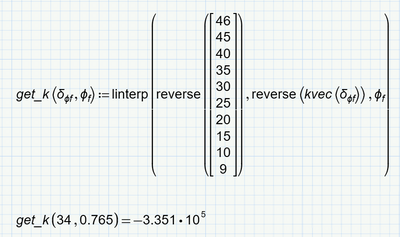
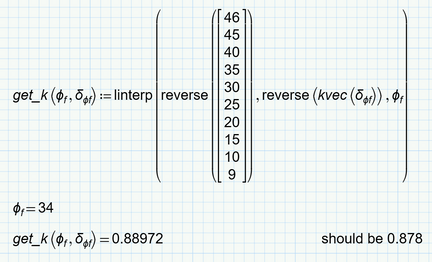
Not sure but can it be that you are looking for something like this:
And why do you think the result should be 0.878?
If I look at the tables with the values Phi.f=34 and delta.Phif you provide, the result 0.89 seems to be correct - slightly larger than the 0.883 the table names for Phi.f=35.
You get 0.878 with the input value 35.616
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner, thank you again for your assistance. That is what I was looking for.
Previous to developing the MathCAD worksheet, I had prepared an Excel spreadsheet that used lookup tables and interpolation. I will have to look at the spreadsheet to see why it is providing a different result.
Thank you!