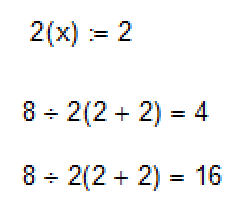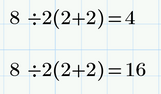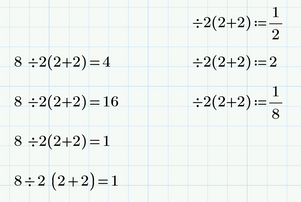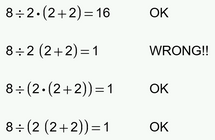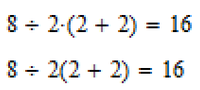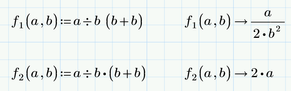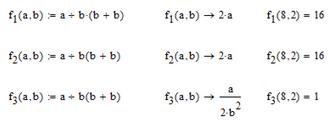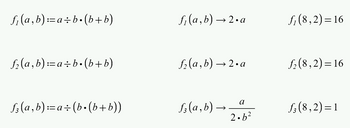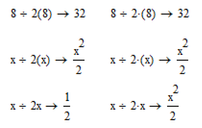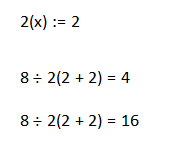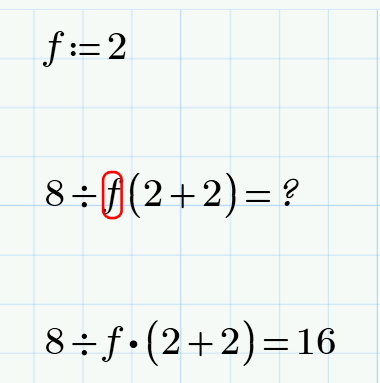Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Only in Mathcad 15
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Only in Mathcad 15
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is Prime:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_E wrote:
Here is Prime:
Attach pls Mathcad Prime sheet!See Mathcad 15 file in attach.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Attach pls Mathcad Prime sheet!See Mathcad 15 file in attach.
The file was never saved and is lost now but I kept a screenshot revealing the bold "secret".
The last line shows how it looks legitimately from a display point of view. You may notice, the on contrary to real Mathacd, the result of prime is WRONG!!!! If we delete the explicit multiplication sign to make an implicit one, Prime gives a wrong result and obviously assumes a pair of parenthesis which is not there! An impicit and an explicit multiplication should give the same result (as its the case in Mathcad).
Unfortunately it seems not to be possible to add a space in a variable or function name (as in your example in MC15).
BTW, the character ÷ can be input via ALT-246 (numeric key pad).
Have you tried to convert your MC15 sheet to Prime? What happens?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think the expression 2(2+2) is being treated by MathCad as a monomial (a single expression), like 2y
2 x (2+2) would be treated as a polynomial.
So, if y=(2 + 2) Then 8 / 2y = 1, and 8 / 2 x y = 16 (PEMDAS left to right operation)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ptc-3007533 wrote:
I think the expression 2(2+2) is being treated by MathCad as a monomial (a single expression),
Yes, and this is what I consider a bug because there should be no difference between an explicit and an implicit multiplication.
BTW, real Mathcad does not show this bug:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
a ÷ b(b+b)
a ÷ b^2 + b^2
Solving for a = 8 and b = 2 could produce
8 ÷ 2^2 + 2^2 = 4
?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ptc-3007533 wrote:
I meant to type =6 on the symbolic
??? not sure what you are referring to.
The symbolics in Prime shows the same bug which is not much of a surprise as the problem is not the symbolic or numeric engine behind the scenes but the user interface and parser which had to be written from anew for Prime.
In Mathcad the implicit multiplication (when you input 8 ÷ 2 (2+2)=) and the explicit one (typing 8 ÷ 2 *(2+2)=) give the same results as it should be. Defining the functions means that we first have to type the expression with a number in front of the opening parenthesis and then replace it by b. Otherwise we would create a function call if we just type b(b+b).
Of course Mathcad delivers the correct result also when using the symbolics.
BUT! While playing around in Mathcad I somehow (don't know exactly what I did) was able to create an expression which show the same error as the one in Prime.
I could not spot any difference between the two (I attach the MC15 worksheet) and so I converted the sheet to Prime (Prime replaced every implicit multiplication by an explicit one) and so we see the structure Mathcad/Prime believes we had typed.
Despite all of this - if we type "8 ÷ 2 (2+2)=" Prime must return 16 and not 1, so I still consider it a bug. Not that severe, as the character ÷ sure will be very seldom use for dividing, but a bug.
Or to show it with a simpler example:
The implicit multiplication should make no difference.
But, alas, here i came across an inconsistent behavior in Mathcad, too, when evaluating symbolically:
Putting parenthesis around a single variable should make no difference.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And here it is in MsWord:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_E wrote:
@LucMeekes wrote:
And here it is in MsWord:
So what comes next? Paint? 🙂
MatLab?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This example is interesting for Mathcad! Why?
See please one typical error in Mathcad:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator