Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Population balance modelling - Rkadapt and Minerr
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Population balance modelling - Rkadapt and Minerr
I'm looking for help solving a problem with a topic I haven't seen any previous example on here of, population balance modeling. In this case the onset of crystallization. The aim is to solve a system of differential equations which represent the crystal population. The first sheet I've attached "Population balance method of moments.mcd" does this reasonably successfully. But I've had to specifty the values for nucleation and growth coefficients (kb, b, kg & g). What I would like to do now is to calculate values for these coefficients so that the model data and experimental data match. The concept is similar to the discussion over here http://communities.ptc.com/thread/43738 were Minerr was used to determine kinetic coefficients to match experimental data. I suspect the issue i'm having is regards to the fact that although the population balance equations are a function of dt, what I'm actually wanting to minise the error for is a function of cooling rate, beta. The second sheet I've attached "Population balance method of moments with minerr.mcd" is my attempt at implementing one of the solutions detailed in the mentioned thread, but my stumbling block seems to be around the programming portion.
Thanks in advance,
Cameron
Solved! Go to Solution.
- Labels:
-
Statistics_Analysis
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, I forgot to attch the worksheet.
Strange enough upon reloading the worksheet I get different results (a better fit and the guess values didn't change much).

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I spot some errors in you minerr sheet
- beta should be a vector, not a range variable
- it seems you have copied the expressions using "augment" from the sheet you mentioned and didn't know what augment is meant for. Augment simply merges together two or more matrices or vectors with the same number of rows to create a bigger matrix. It doesn't make any sense to apply augment to a single vector, the output woul be just that vector again.
Was the intention that MinErr should try to make DeltaT.max equal to DeltaT.max_exp? How could that be? You supply 19 different values for better, so the first vector would have 19 elements, while the second you have defined with only 12!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If i set beta equal to beta_exp then that would create at vector both with 12 elements correct?
For the given statement then, if it's only a single vector should it just be a case of:
Delta.T.max(beta, kb,b, kg, g) = Delta.T.max_exp?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If i set beta equal to beta_exp then that would create at vector both with 12 elements correct?
Yes beta (not "better", as I wrote in the last post) just has to be a vector the same dimension as DeltaT.max_exp.
But doesn't it matter for you which values are in the vector beta?
For the given statement then, if it's only a single vector should it just be a case of:
Delta.T.max(beta, kb,b, kg, g) = Delta.T.max_exp?
Yes, but you would have to use vectorization on th LHS. To further explain: If beta is a range variable as you had, feeding beta in DeltaT.max results in something which looks like a vector on display, but it isn't. You can't access single elements (as in a range) and you even cannot assign it a variable. So you cannot compare it to a vector, too.
If you feed a vector in a function, it depends on the operation in the function if the result is a vector or something else. For example f(x):=x^2 and g(x):=x*x. If you call f and g with a vector as argument, f will return a vector with the single elements squared and g would return a scalar (the dot product of the vector with itself). To avoid this you have to use vectorization.
I attach a sheet which seems to work, but the fit is awfully bad. I tried with somewhat different guess values and got the same result. Maybe the guesses and/or the model needs a rework.
I provided an alternative for your way to calculate DeltaT.max which has to call Rkadapt only once and not five times as with your solution. Nevertheless the solveblock still will takes its time, especially with N set to 1000 or even more (N influences the outcome as I noticed because while testing I had set N to 100).

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, I forgot to attch the worksheet.
Strange enough upon reloading the worksheet I get different results (a better fit and the guess values didn't change much).

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks! It does exactly what I'm after. The model as a whole seems quite senstive to a number of the variables. I'd see that N affected the outcome too. At the moment I made a slight modification to the cooling rate expression, changed it to 0.12i to tend towards the higher cooling rate and ended up getting a fit that looks pretty good:
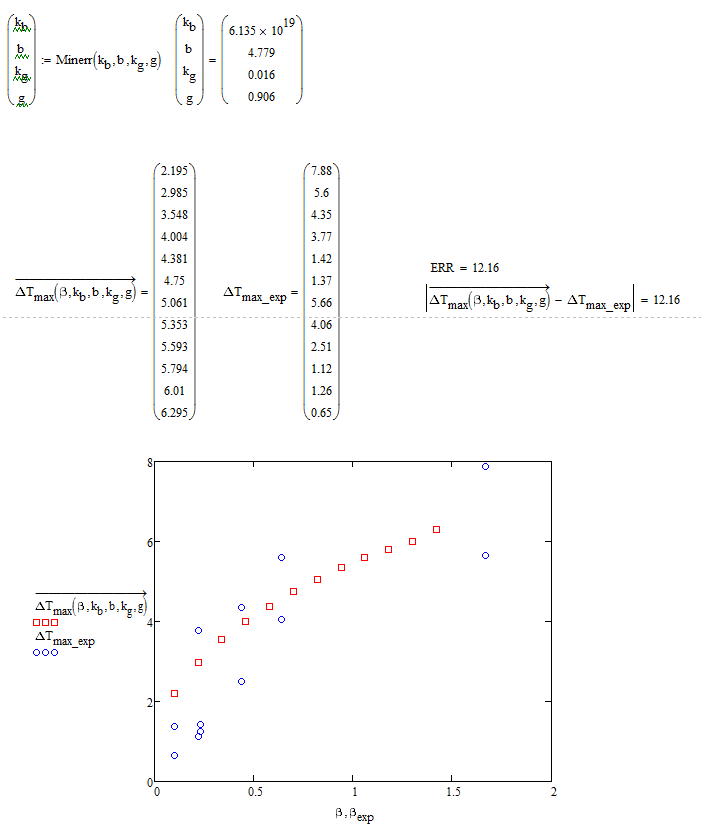
At the moment it's matching the experimental data only on the temperature at the onset on crystallization but potentially I could add the particle size. Although I'm still working out how to extract the particle size from the moments. Going to mark this as answered.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I tried with different beta's, too, but it seems my goal ws going up to high (in the region 1.85 where your original values were) but found that simply cuttin of the higher values as I did yielded better results. You are right, the model seems to be rather sensitive.
You could of course define the vector beta in a similar way as beta_exp so you are free and not restricted to equidistant values.
I tried beta:=beta.exp as you suggested in a prior post, but the result was inferiour.
What you have found seems to be the best fit (while still not necessarily a real good one).


