Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Preventing System Failures with Reliability Testing for Pump Systems
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Preventing System Failures with Reliability Testing for Pump Systems
By D.M. Griffin, Jr.
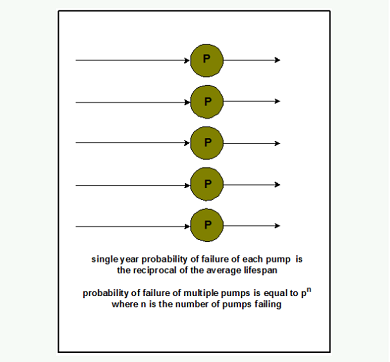
- Determine the number of pumps needed so that the probability of not having a system failure during a three year period is more than .95
- Apply in Mechanical Engineering, Mathematics, and Statistics
- Perform using probability of system failure (system reliability), probability, binomial random variable, reliability, Bernoulli trials, etc
This worksheet shows you how to determine the minimum number of pumps needed so that the probability of not having a system failure (system reliability) during a three year period is more than .95. This worksheet uses the example of a pumped storage power supply scheme that has five identical pumps in parallel. One is capable of system operation and the others are backups. The mean life span of these pumps is 10 years. For this problem, you can assume that all the pumps in the parallel must fail before the system fails in a given year.
To begin, the worksheet shows you the thought behind the probability of a 1,2,3, and 5 pump system failing within three years. Next the worksheet shows you how to conduct 3 Bernoulli trials for each year. The probability of failure during each trial depends on how many pumps have to fail before the system fails. The worksheet calculates the:
- single year prob
- ability of a 1 pump, system failure when there are 5 pumps operating
- single year probability of failure of system when 4 of 5 pumps are required
- single year probability of a 3 pump failure in a three year period when 4 of the 5 available pumps are required for operation
The worksheet also shows you how to calculate for each system's reliability along with the probability of failure. All notation, images, data, formulas, calculations, and solutions are provided to aid you in your own calculations.
Download and explore this worksheet yourself! You can download a free lifetime copy of PTC Mathcad Express and get 30 days of full functionality.
- Labels:
-
Mechanical_Engineering


