Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Problem with ODEsolve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Problem with ODEsolve
Hello everyone!
I have a question, how can I solve a system of equation, which is consists of three equation (two of them are Differential and other one is not) using ODEsolve or there is some other way?
So I had a system of two differential equation and everything worked just fine, but then I need to add one more equation and this equation is not differential. So I don't know are the ODESOLVE able to solve this kind of systems or not. It keeps telling me, that I have too few initial conditions. File 9 is a file where only 2 equation are solved.
Thanks for your help
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Vladimir Novikov,
first of all you should do the following changes:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
.) The whole sheet is unitlesse - otherwise I guess we would experience severe problems with odesolve in Mathcad 15 (thats better in Prime). So Vladimir decided to write the supposed units next to the values in a textbox or separate math region for documentation and reference purpose only. This has no effext on the calculations.
I guess Valery would define every unit as being :=1 and then attached them in the unit field.
.) the equations with the "j" also are for refernce purpose only and have no effect on the calculations.
At the moment I haven't digged far enough in the calculations to be able to provide a solution but I guess the problem is, as Vladimir already guessed, that one of the equations is not an ODE.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would say that not all the units are written in text boxes, on the contrary, many are written as if they were variables. The first (° C) for sure.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
it is not affecting calculation at all, units are not the reason of problem 100%
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F.M. wrote:
I would say that not all the units are written in text boxes, on the contrary, many are written as if they were variables. The first (° C) for sure.
I wrote, that the units are placed "in a textbox or separate math region". For the °C the latter applies. None of the units you see are in play in the calculations!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yes you right. all the units and equation with j it's just cosmetic things for report, real calculation begin after given and in given find block everything seems to be defined properly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I was attaching:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for making my units look not only good and proper but translated from Russian language))) but it is not the case of my problem. My problem is related to finding solution for system of three equation (2 of them is ODE and one is not). I'm looking for a way to solve this system and seems that odesolve is not working properly for this problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F.M. wrote:
I was attaching:
Why? We have the sheet from the OP and I guess adding the units did not solve the problem the OP is facing, right?
On contrary - adding units makes it worse as odesolve will not work, even if if the rest would be OK.
You may give it a try: Use his sheet 9.xmcd, which is working OK, add the units where you think there should be units and see, if the odesolve-block still works OK.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The things you referred to is not involved in calculation process. Yes, I made my units as a separate text boxes, which is guarantee, that it not going to mess up calculation. Also you said that j is undefined, that's true. But in the equation block there is no calculation at all, so j is not involved in calculation, but in given-odesolve block I change j (mass flow) with Maxwell equation for mass flow.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
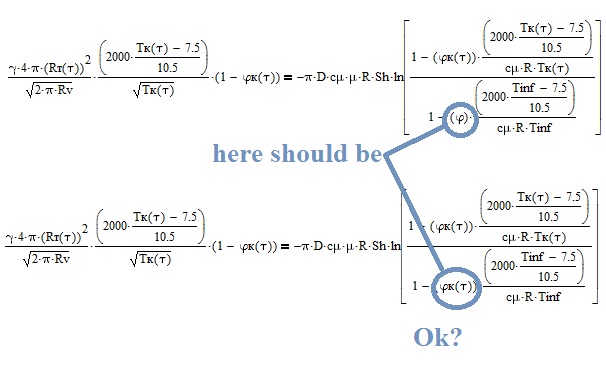
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is the solving block. This system of equation describes evaporation process of spherical drop. The first equation is about changing its temperature during evaporation. The second one is about changing its radius during evaporation. The third is about changing of humidity. So phi in this last equation is relative humidity. The phi is the relative humidity far away from water droplet and it is constant and phiк(tau) is the relative humidity near droplet it is unknown value and i need to find it. I wanna have it like the function of tau (time). So i think i should somehow rewrite the third equation as Zero-order differential equation if it possible.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not sure. I noticed it, too, but left it in place because phi is a defined variable (0.5). So I guessed its there on purpose. But chances are that this phi simply is left over from the simpler version in sheet 9 and really shoul be the function. I'll see if my unsatisfactory solution performs better with that change.
The OP will clear the questions.
EDIT: Making the change you suggest makes the solve blocks perform much better and faster, but RT and TK now are constant functions 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Attach is an absolutely unsatisfactory solution by turning phik into a function in an extra solve block.
I had to limit tau1 because of a strange error if its too large and the phi solve block takes quite long to calculate for higher values of tau.
Maybe its a tolerance problem because of too hight or too low values - when I set TOL to a lower value liek 10^-9 the odesolveblock fails for lower values of tau1, too.
Hope somebody has a better idea to tackle with that system.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for help, but I need something little bit different. The main idea is to get a function of phik(tau) from the third equation to insert it in two previous equations. So I will get function of temperature and radius related to changing relative humidity (phik).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, if my solution would work OK, which it obviously doesn't, you could, after solving for TK and RT, define phi_k(tau):=phik(TK(tau),RT(tau)) and you have the demanded for function. A bit inefficient, as the every call to this function phi_k would call the odesolveblock twice.
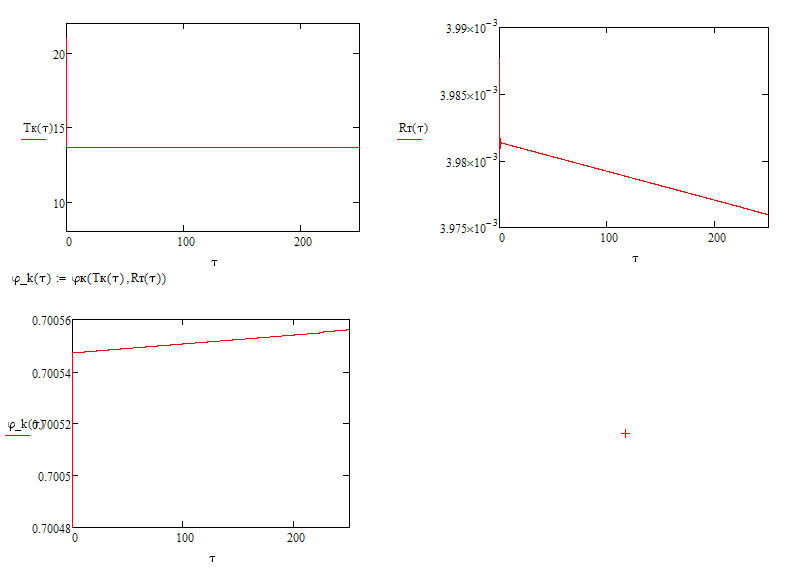
Here is what I get with tau1=250 AND TOL=CTOL=10^-3.
Setting CTOL to 10^-4 or lower and/or TOL to 10^-6 or lower makes the block fail (lower values for tau1 work OK). This may indicate a convergence problem. Cause could be values near the limits (too large or to low) or a problem with the equations used.
There seems to be an abrupt jump right at the beginning.
Not sure if thats what you expect. If not, you may wish to check your equations.
For whatever it may be worth I attach the sheet with the settings for CTOL and TOL which work for me and added phi_k at the end.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
your solution doesn't seems to work fine for me(((
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vladimir Novikov wrote:
your solution doesn't seems to work fine for me(((
Yes, The solution sure is unsatisfactory. I guess that you had changed the value of the system variable TOL from the default 10^-3 to something smaller. Try TOL:=10^-3 at the top of your sheet.
You may also set tau1 to a value lower than the 250 which worked for me.
But as your original sheet demanded to solve up to tau1=2000 (or was it even 20000?) I guess this would not be a satisfactory option.


