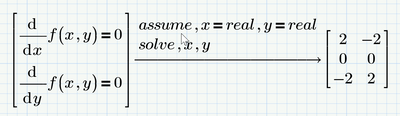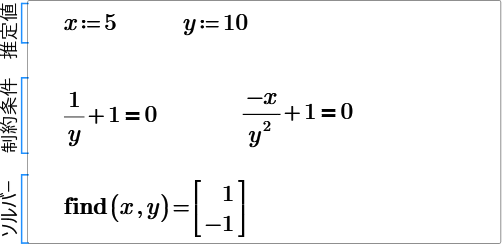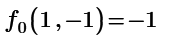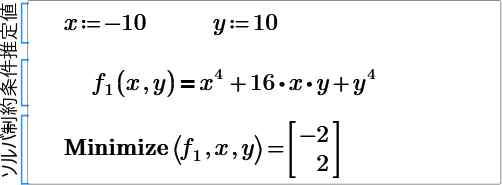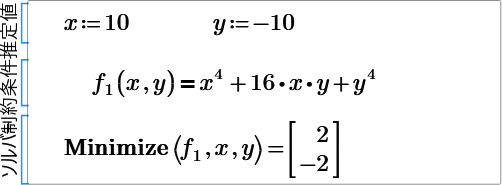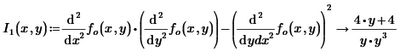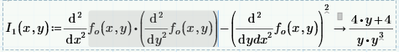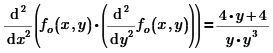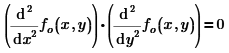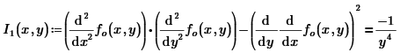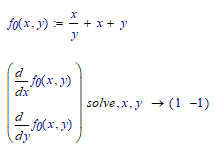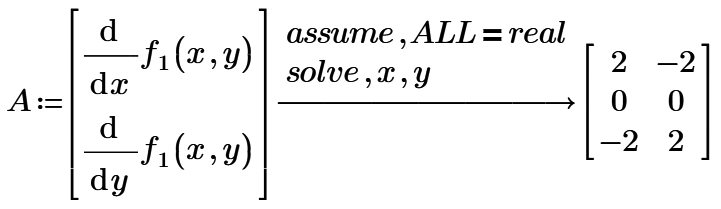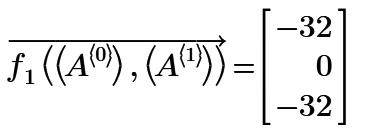Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Problem with finding stationary points of a partial derivative function and guess values
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Problem with finding stationary points of a partial derivative function and guess values
Hi all,
I hope all of you are enjoying life!
I am working on finding the stationary points of function of several variables f(x,y).
Problems:
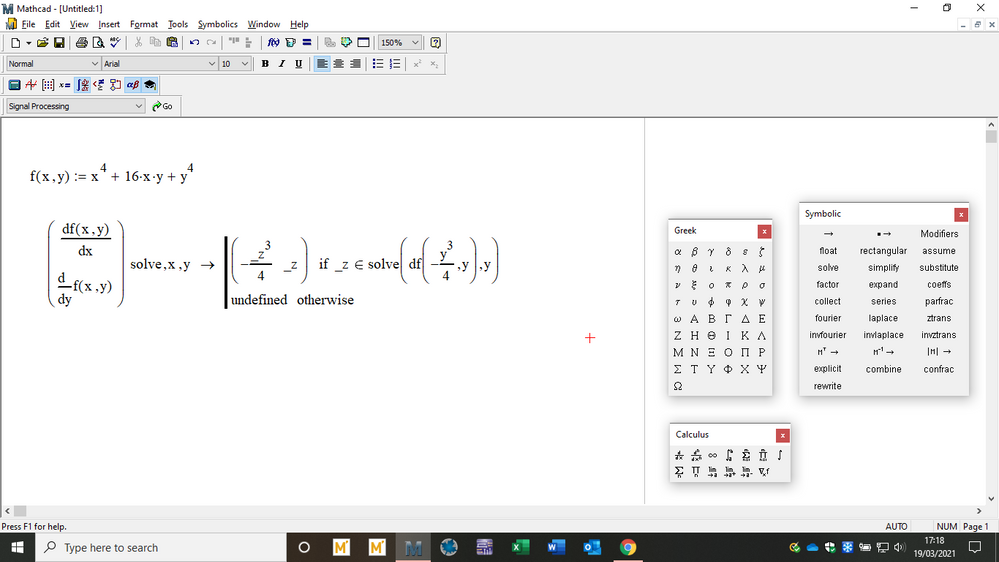
1- How do I solve a system of equations without knowing its guess values? I took me a while to get the values x=5 and y=10 otherwise the equation solver does not work.
2- It seems that I have inputted the equations wrong to find the nature of stationary points ? Can anyone give me advice or tell me why is this not working? So, I1 should be a negative number(I think)
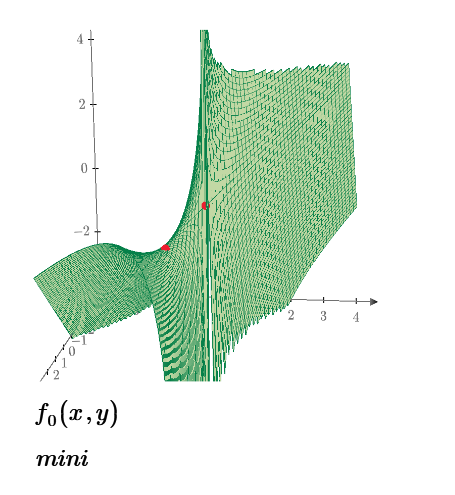
The correct answer is: a saddle point at (1,-1) [according to the maths textbook]
(Update: problem 3: how do solve an equation that has more than one solution? when I used solve block it only returns one solution)
Please have a look at my worksheet.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Primes infamous auto-labelling feature often is more a PITA than helpful.
You have to manually label the variables after "solve" to be "Variable" and NOT "(-)" (automatic).
And in case you are not interested in the non-real solutions, you may add an appropriate assume modifier:
If you make f an additional argument of "HesseDet", you may use this very same function for any of your given functions without having to redefine any more.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- Prime 7.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Thanks for the reply!
Why does it not work when I use the formula shown in the maths textbook? So, saddle point should give an answer less than zero in that equation in the screenshot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The saddle point is [x,y,z]=[1,-1,-1] Another point is [0,0,0], which is left above, is not saddle point,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You made two mistakes.
The first term is incorrect, because you've placed the second derivative to y inside the argument of the second derivative to x. This is hard to see from a picture, but by selecting portions you can find out how Prime interprets what you typed. It's this:
Which means as much as:
Whereas you should have:
But as soon as you put brackets around the derivative to y, Prime appears to assemble it under the derivative to x. Be careful with this!
The other error is with the last term, which means the second derivative of fo(x,y) to the variable ydx. Now ydx is not a parameter of the function, so this derivative yields 0.
The total result is therefore only the result of the first term.
You should have had this:
Then I1(1,-1) gives -1.
Success
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks LucMeekes,
I want to ask is there any way of solving a system of equations that results in all the solutions? If the solve block is used, one has to play around with the guess values to get all the solutions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sure there is. If at all possible you should first approach such problems symbolically.
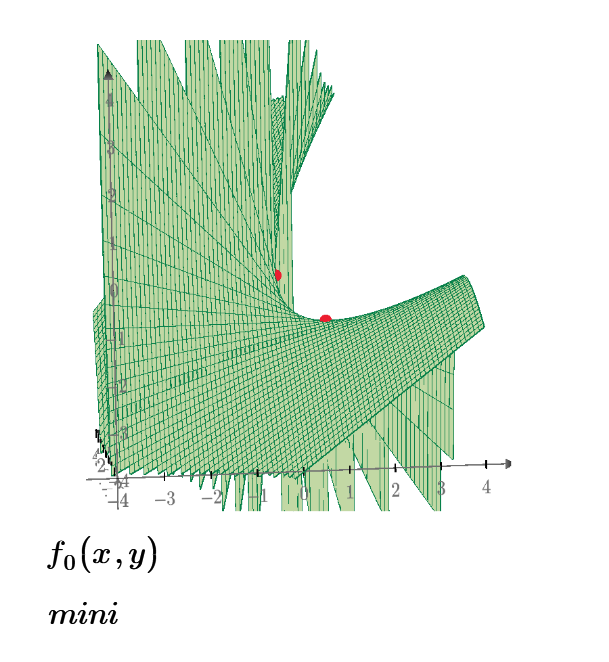
For f0 you have all the solutions:
There is only one.
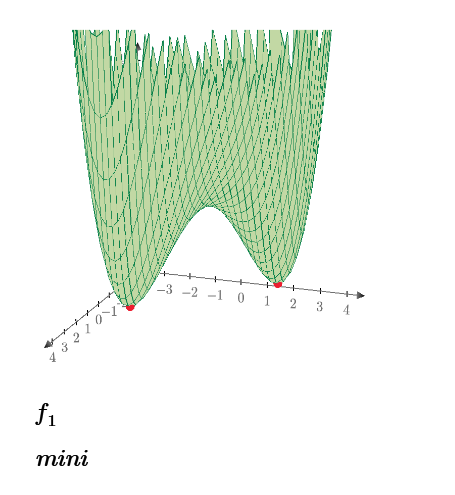
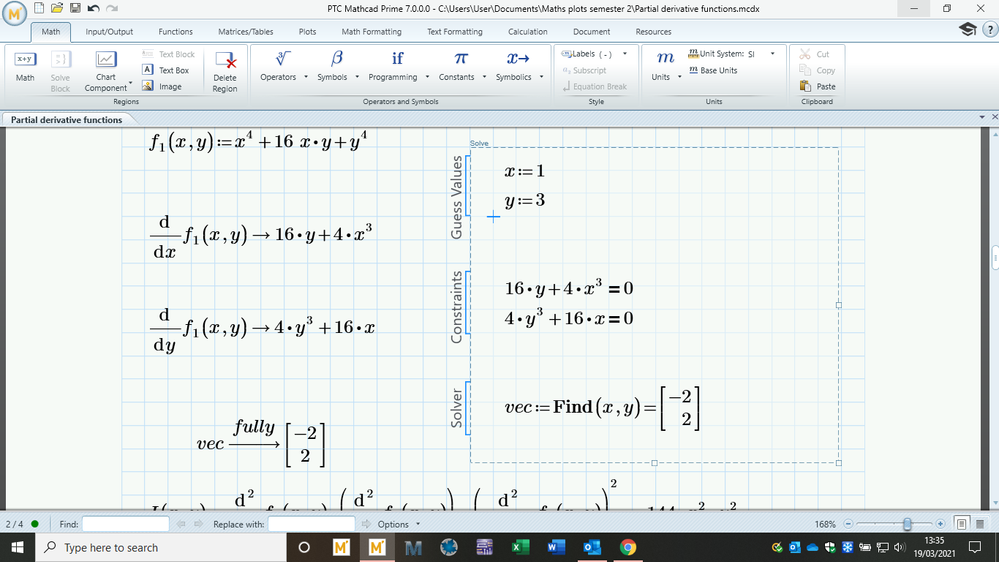
For f1 you should get something like:
if necessary add 'fully' to the solve directive.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ok thanks. It seems that using 'fully' does not work when using solve block, it does work when storing the equations in a vector like you have.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just one more question: where do all these complex solutions come from, does it have infinite solutions?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
'fully' is a keyword for the symbolic solver. Prime does not have a provision to solve solve-blocks symbolically so you cannot use it there.
There are not infinite solutions for the f1 function because f1 does not involve periodic functions, just the 13, some of which involve complex numbers.
You should try to replicate my example for f1 in your Prime; Create a vector of two elements and put in the two derivatives of the f1 function, then symbolically solve that for x and y. (I can't do it, I don't have a license for Prime, am limited to Prime Express, and so cannot use symbolics. But I can always open and view your Prime sheets. My work is generally done in Mathcad 11, that's why it shows differently.)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Lucmeekes,
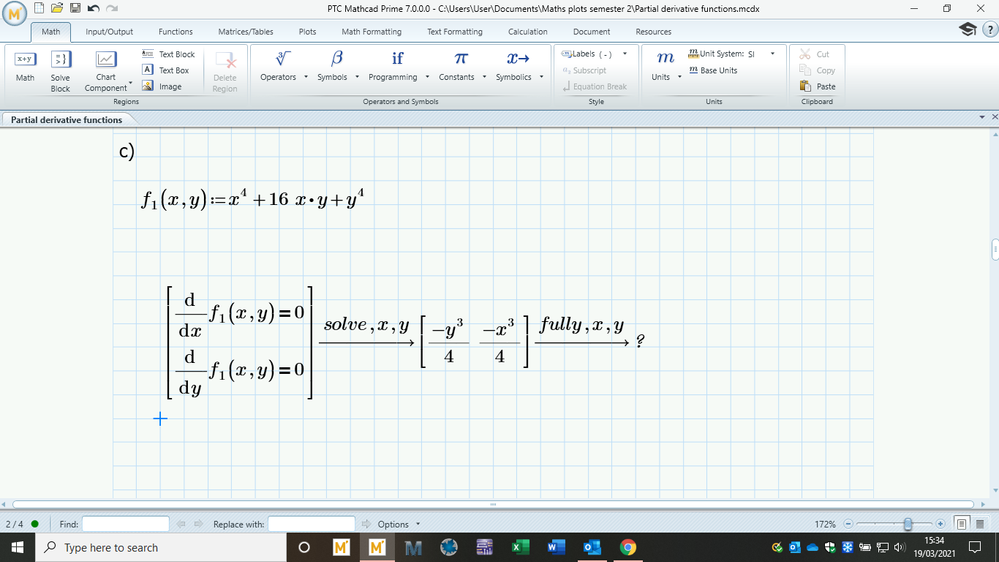
So I copied exactly what you did however it did not work, then I tried making it equal to zero but still no answer. Then I tried using 'fully' but now it doesn't work at all, it returns with a question mark. I attached my worksheet(please go to part 'c)' ignore the rest they might have mistakes from earlier.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime has this wonderful feature of autolabelling. This serves to change m to a unit m, for metre, kg to a unit kg for kilogram. It also detects sin and recognises it as a function sin, etc.
So it will automatically assign a label to whatever you type. This is great, but everything that goes automatically CAN (and as Murphy will have it) WILL go in error (sometimes, or often). It's what happened here.
Check the labels of the x and y as arguments to function f1, and compare that to the labels of x and y that follow the solve keyword. Make them the same if different and see what happens.
Best is to have them all labelled as 'Variable'. Note that a label '(-)' means 'automatic'.
Regarding 'fully': That is not a separately usable keyword, but MUST follow 'solve' keyword. So if you need it, type it after the variables you are solving for like this:
solve,x,y,fully
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I changed the variables and started a new worksheet just in case; however I don't get the full vector of solutions like you did in mathcad 11.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Primes infamous auto-labelling feature often is more a PITA than helpful.
You have to manually label the variables after "solve" to be "Variable" and NOT "(-)" (automatic).
And in case you are not interested in the non-real solutions, you may add an appropriate assume modifier:
If you make f an additional argument of "HesseDet", you may use this very same function for any of your given functions without having to redefine any more.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Also, what did you define before that made it work? I tried this in the 'real' mathcad and it doesn't work. Can you send me your file if possible.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your partial derivative to x doesn't seem right...
If you want help, post your worksheet, not just a picture.
(And if you want me to be able to open your Mathcad 15 work, save the worksheet to Mathcad 11 (.MCD) format and post that. Don't mind any warnings on the save...)
Attached is my sheet, which should work in Mathcad 15, and you should be able to translate it to Prime7 using the converter supplied with/in there...
I've also modified your Prime sheet, just for the f1 function. See if it works.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I have already attached my file previously.
I have attached it again, I NEED help with finding all the solutions which are (0,0) (-2,2) and (2,-2). How can I do this? I want to get all the solutions like you did previously that gave all solutions including complex.
I stored the equations in a vector and used fully but does not work.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't see your mathcad 15 sheet attached....
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
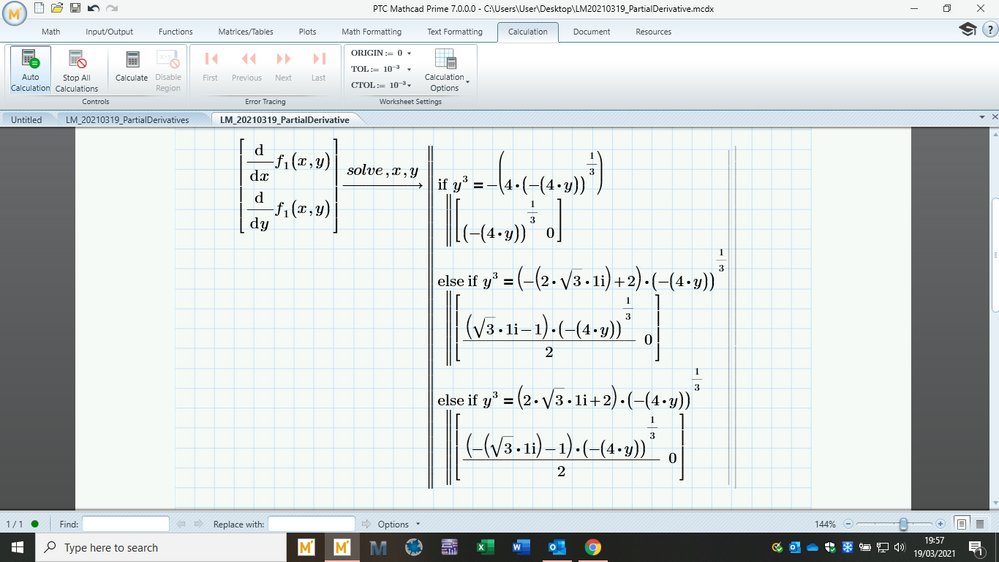
It does work now finally, but it seems like it cannot be done on MP7. I had some issues in the derivative maybe that's why. I think I might just use this old mathcad. I don't like using this old version but I might just have to........for example this comes out blurred but once you click on it; it becomes clear
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yeah so I tried the prime sheet you attached and it gives a dirty else if function, I dunno what any of that even means. I think just forget it, this is not going anywhere I will use the older mathcad.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I cannot open P7 sheets but what your picture shows, again seems to be a problem with Prime's autolabelling.
See my answer above where you have to manually change the label
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- Prime_7.0