- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Programming Challenge - Most Prime Mathematician!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Programming Challenge - Most Prime Mathematician!
Following on from Valery's observation on Pushkin in one of the Euler Problems (Re: Programming Challenge - Project Euler - Problem 10), I wondered which mathematician (whatever) lived through the greatest number of prime years, and this suggested an immediate challenge.
To keep it simple, we'll take account of the well known fact that in every year since 0 AD (0 CE), at least one mathematician has been born who lived to be 100 years old. What year was the mathematician born who lived through the greatest number of prime numbered years?
In the event of more than one birth year resulting in the same maximum number of prime years, what year was the first year such a mathematician could have been born in, and what year was the last possible year.
In the first instance, you can include any (future) mathematicians born no later than this year (2016).
You may assume in the second instance that the end date for the challenge is this year (2016), so any mathematician born this year cannot have lived through any primes.
Stuart
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
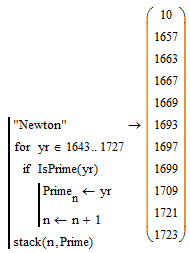
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Given the higher density of prime years in the first century compared to other centuries, I would assume that the solution to your question would be someone who lived from year 2 to year 102. Year 3 to 103 would have an equal number of primes.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Modern mathematics wear pants of this fabric:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Indeed, the lowest numbered years do have the most primes in their centuries. There's an interesting dip at 1322 though ...
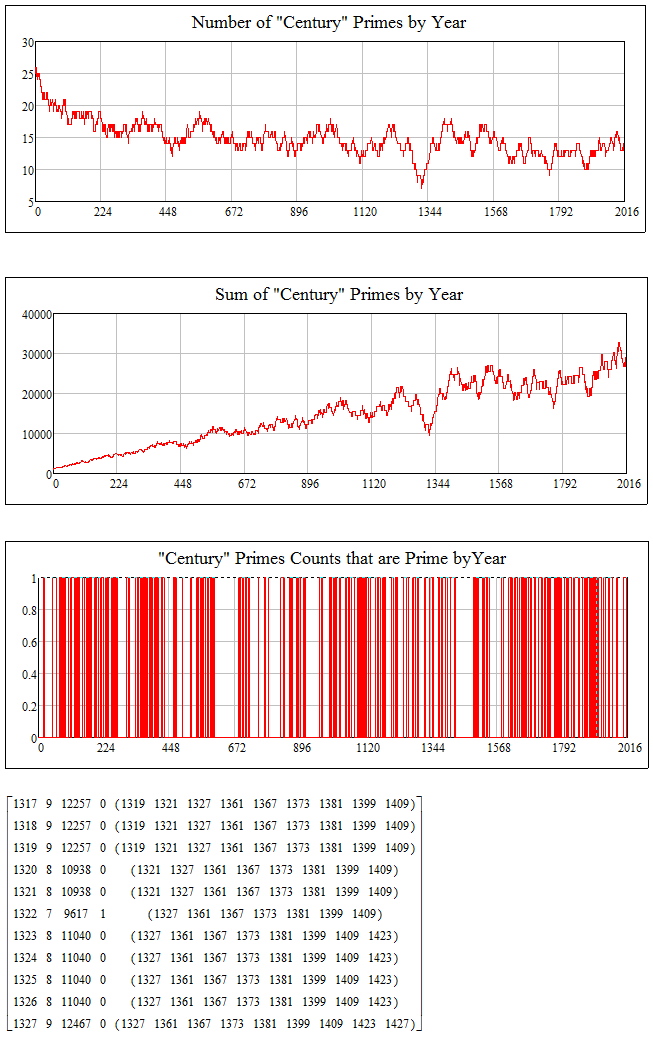
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
Indeed, the lowest numbered years do have the most primes in their centuries. There's an interesting dip at 1322 though ...
Extra imaginary points for determining the first year tha has fewer primes than 1322 ....
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Extra imaginary points for determining the first year tha has fewer primes than 1322 ....
5904 with just 6 Prime years
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark is right of course.
Mathematicians born in the years 1, 2 or 3 (assuming the get 100 years old) have lived in 26 Prime years which is the maximum to achieve.
Maybe its better to ask for the minimum number. The solution is unique -> Year 1322 with just 7 Prime years in the following 100 years.

Additional challenge: What is the first year with 0 Prime years within the next 100 years?
(Hint: Its a 6-digit number !)
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
Maybe its better to ask for the minimum number?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Werner Exinger написал(а):
Maybe its better to ask for the minimum number?
You are solving a different puzzle. You misunderstood Stuarts challenge! We are only dealing in this thread with people who got exactly 100 years old and are assuming that at least one such person is born in every year! Thats the challenge.
Read again Stuarts initial post, it says:
"To keep it simple, we'll take account of the well known fact that in every year since 0 AD (0 CE), at least one mathematician has been born who lived to be 100 years old. What year was the mathematician born who lived through the greatest number of prime numbered years?"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, Werner, I know it.
Two puzzles are better then one!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Thank you, Werner, I know it.
Two puzzles are better then one!
Really!? So I would say that two threads for two different puzzles are better than one for both. You already posted a lot of that kind in Stuarts Project Euler thread.
My suggestion to ask for the minimum was of course still assuming Stuarts initial rules concerning century mathematicians.
The same applies to my add on challenge of finding the first year with zero primes within the next 100 years
Sorry, but people like me tend to get confused by off topics or significant rule changes during a game 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hope this helps minimize the confusion. I've created a thread for Prime Real Mathematicians (as opposed to my notional centenarians) - there are even a few who've strayed over the 100 year mark.
Programming Challenge - Most Prime Actual Mathematician!
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a functional/"programmed" approach (still using Stuarts primes(n) to precalculate a list of primes)




