Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Rectangular plate vibration in Lame mode
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Rectangular plate vibration in Lame mode
Hello everyone,
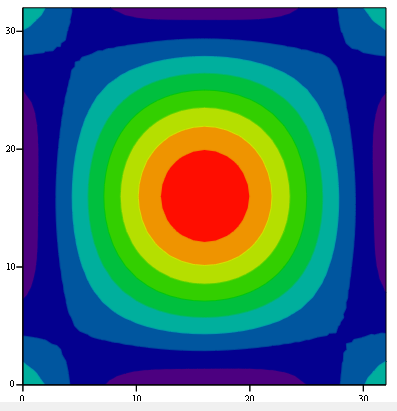
I'm trying to solve a system of partial differential equations corresponding to in-plane vibration of a thin plate in Lame mode. This is one of a papular resonance mode in microelectromechanical systems (MEMS) devices. An example of the displacement profile of Lame mode is shown in the attached worksheet.
For the boundary conditions, the plate is fixed at the four corners, so the displacement U(x,y) and V(x,y) along x and y-axes are zero (in some references, also the center is fixed). On the sides, the normal components of stresses are also zero.
Gathering all the boundary conditions, I'm still unable to proceed with "Pdesolve" routine and get the displacement and natural frequency.
Could anyone make a suggestion for resolving this problem? I highly appreciate your assistance.
Payman
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
This has taken a long time to verify against a commercial software suite Strand 7.
Enclosed is 3 zip files zipped into an over arching archive.
PlateVibration.zip are Mathcad worksheets.
References.zip are PDF references that show how finite elements work and some examples
Strand7_Files.zip is the commercial package files. A free viewer is available at
The files with extension lsl and nfl are log files and are text. nfl standing for natural frequency log shows the results.
In summary the Mathcad worksheets perform natural frequency analysis of a rectangular plate with varying support conditions and can plot mode shapes for each natural frequency.
It has reasonable accuracy.
Enjoy
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
" I'm still unable to proceed with "Pdesolve" routine and get the displacement and natural frequency."
What you describe is two problems. Displacement under load. Vibration at natural frequency where you solve for the frequency but the displacements values at that frequency are unknown but the displacement pattern is known. I notice you define no "loads" for displacement under load.
I have the solution for you for natural frequency supported at the four corners by finite element analysis but it will take a day or so to transcribe from a worksheet that solves for displacement under load.
In terms of your Mathcad solution you need to define "U" and "V".

Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Terry, I appreciate your help and I'm eager to receive your hints.
All the best,
Payman.
PS: I modified the worksheet and posted the new one.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Does the reference you are using dimension the thickness of the plate as well as the plate plan dimensions 700 x 10^-6?
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
the thickness of the plate is 17 microns and the lengths of the square are 700 microns.
Bests,
Payman
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I need a little more time with this problem.
Finite element analysis was developed for analysis of airplane structures at an American airforce base in the 50's and 60's. It may not be applicable to a 0.7 x 0.7 x 0.017 mm chip.
It works to known solutions when solving for static problems of load and displacement even at such relatively small scale..
It does not seem to work when solving for natural frequencies of vibration against known equation solutions.
I think it is ill conditioned matrices when solving the eigen value and eigen vector solutions.
I am having the same problem on a commercial finite element software package as I am having with the Mathcad implementation. So a little more time investigating is required.
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
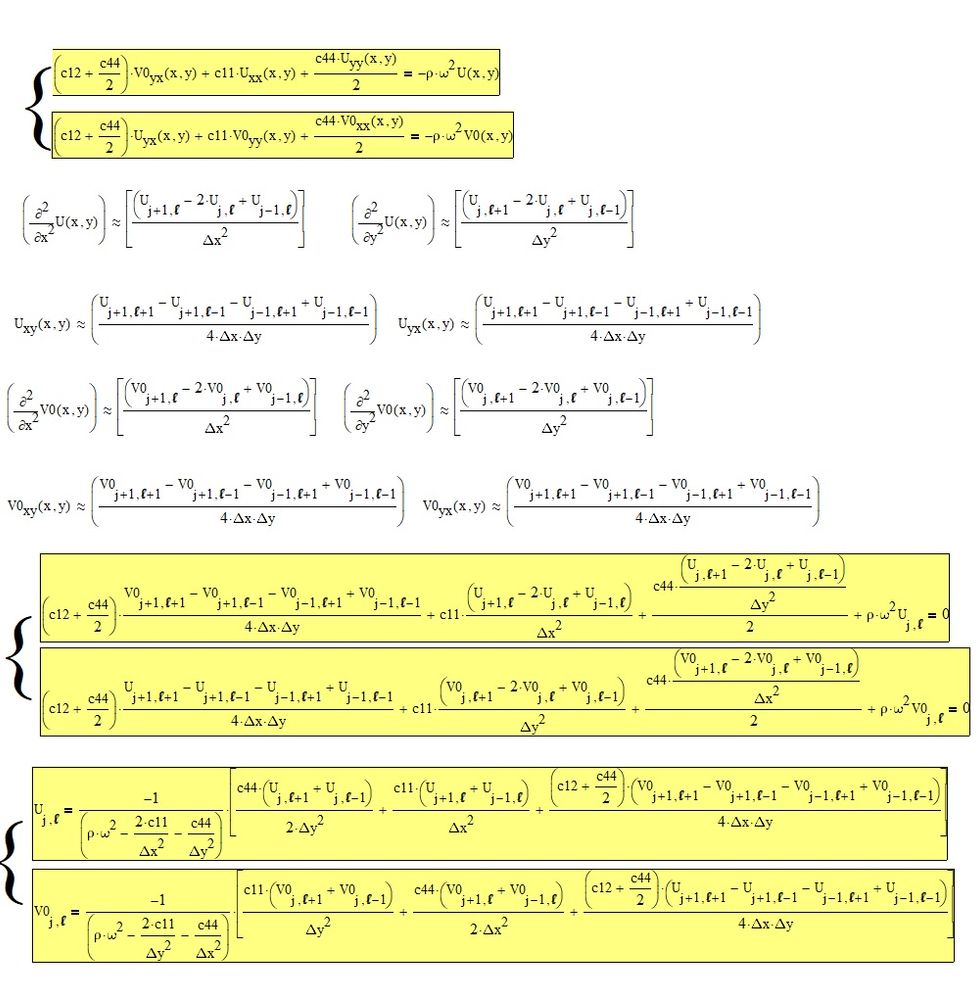
Hi,
You could use the finite difference method instead of pdesolve. In this way the problem is clearer and, then, maybe you could even try using pdesolve. A suggestion how to do it is in the following photo(how to define omega?) :
... the most challenging part comes later.....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Topaz,
I truly appreciate you. This is a great help to start. I'll consider this approach in the following days.
Thanks again,
Payman
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
This has taken a long time to verify against a commercial software suite Strand 7.
Enclosed is 3 zip files zipped into an over arching archive.
PlateVibration.zip are Mathcad worksheets.
References.zip are PDF references that show how finite elements work and some examples
Strand7_Files.zip is the commercial package files. A free viewer is available at
The files with extension lsl and nfl are log files and are text. nfl standing for natural frequency log shows the results.
In summary the Mathcad worksheets perform natural frequency analysis of a rectangular plate with varying support conditions and can plot mode shapes for each natural frequency.
It has reasonable accuracy.
Enjoy
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is a great job, thank you, Terry.
It will take some time to digest it.
All the best,
Payman
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
This file shows two new things
a) How to clamp the top,bottom,left,and right edges of the plate as part of the finite elements.in terms of dx,dy at top of sheet. By altering these boundary restraint codes all the support cases in RICE0523.pdf tables can be achieved.
b) Comparison to RICE0523.pdf tables.
The file uses a poissons ratio of 0.3 so comparison to RICE0523.pdf tables is possible.
b) Comparison to RICE0523.pdf tables is good.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator