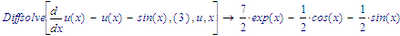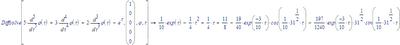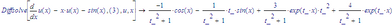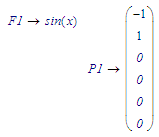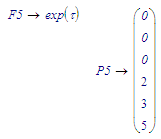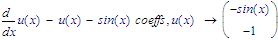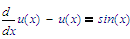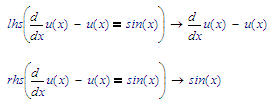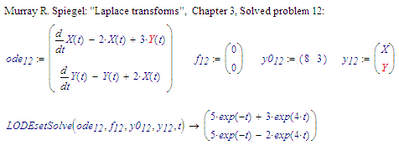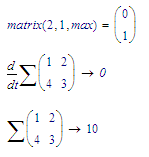Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
SYMBOLIC Differential Equation and System of Differential Equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
SYMBOLIC Differential Equation and System of Differential Equation
Hello,
There is a function that can solve SYMBOLICALLY a differential equation and a system of differential equations automatically in Mathcad?
Or at least, how can I solve SYMBOLICALLY a differential equation or a system of differential equations (automatically) in Mathcad? But without using manually Laplace Transform for each term or Odesolve(-numeric/graphic), but rather something automatically...if exist...
Thank you.
Solved! Go to Solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe my reply was done too fast.
It looks like your sheet is working OK despite of the errors noted.
I attach a pdf print of your file after recalculation and after separating the overlapping regions.
Nice work, indeed!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ha, that's nice. Thanks for checking.
Now on to, task 2:
I have one implementation in Mathcad 11 that allows:
And on the other LODE it returns:
So I guess it's done.
Well, almost... I'd like to make sure that the coefficients of the derivatives don't contain the independent variable. Because if they do, you get the wrong answer. Prof. Birkeland's polynome does not account for that, and I'm certain it's not easy to implement support for it..
Example:
this is not the solution.
In the attached file is a routine GetODEparts, with some examples next to it.
Please check if it runs in Mathcad 15. These are the expected results:
Thanks,
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks!
Does not look good, unfortunately. The result on Page3 does not meet my expectations.
The P1 and P5 values are OK.
The result for F1 should be just sin(x) and should NOT include any (derivative of) y_(x).
Similarly for F5, it should only be exp(tau).
Apparently MuPad, when requested to provide the coefficients for y_(t_), includes the derivatives of y_(t) with the other stuff that's not dependent of y_(t_). Maple doesn't do that:
(Where -1 is the coefficient of u(x), and -sin(x) is everything independent of u(x))
Though I must say, I can't blame MuPad for doing that. It may be the correct answer.
But it does mean that it's going to be harder to filter the particular function out of the LODE expression.
Does Mathcad 15 provide for a symbolic lhs() function (That takes the left-hand-segment of an expression, everything that is to the left of := or = ) and the rhs() function (or symbolic keyword)? If that's the case, it may be possible to supply the LODE as:
and do:
If not, the differential equation solver function will (need to) require that the particular function is supplied as a separate argument (as it does in Prof. Birkeland's function).
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I see the problem and I fear that Mathacd does not provide a LHS or RHS function/operator (similar to numer() and denom()). I would have needed them quite a couple of times when trying to automate the manipulations of an equation.
And you are correct about the working of the coeffs keyword and I, too, think that is correct from a math point of view. On the other hand - its wrong if u(x)=exp(f(x)), for example 🙂
Its not possible to give a correct result without knowing u(x), in fact.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now I wonder if this works.
Please check attached.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello @Werner_E ,
can you please convert the two files to (Mathcad 15) .xmcd files, check if the functions still work, and then attach them in a reply?
Thanks!
Luc
The final result is posted here:https://community.ptc.com/t5/PTC-Mathcad/Solving-Ordinary-Differential-Equations-symbolically/m-p/689336#M192090
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fine work! Sure something to keep in ones toolbox.
Find attached the two files converted to MC15 *.xmcd and also the pdf print of the example file.
I had to vertically separate the regions in the LM_... file so they won't overlap.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's done:
Now neat it up and transport to Mathcad 15.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can you check if this works in Mathcad 15 with similar results to Mathcad 11 (pdf attached).
If it does work, please save both files as .xmcd.
Thanks
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Unfortunately ODE systems don't work. The error message is an less helpful "pattern match exception".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, now it becomes tapping in the dark.
Please try the attached.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry! Same error again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Installed a trial of Mathcad 15 and found out that, where this is posible in Mathcad 11:
Mathcad 15 is more restrictive:
The issues are resolved now, and the result is posted in https://community.ptc.com/t5/forums/replypage/board-id/PTCMathcad/message-id/192090.
Luc
- « Previous
-
- 1
- 2
- Next »