Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solving non-linear initial value problem (ODE) with Solve Block
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solving non-linear initial value problem (ODE) with Solve Block
Hi,
I am trying to model a moving fluid interface in an annular pipe for a varying cross-section. My model is based on a modified Poiseuille equation. If I use a constant cross-section, then MathCAD solves my linear ODE just fine and I get results as expected. If I consider a varying cross-section however, then my ODE becomes non-linear and I'm unclear on which format MathCAD requires to solve this.
All unknowns in my attached file are constants, except L(t).
I'd be very thankful for any help on how to format a non-linear ODE of this form within a solve block.
Regards,
Alex
Solved! Go to Solution.
- Labels:
-
Mechanical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
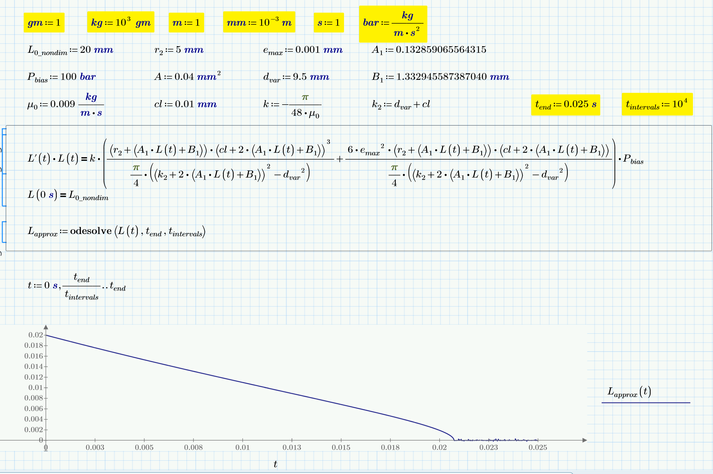
Obviously it has to do with the units and/or their magnitude.
I changed the values of the "unitless units" on top of the sheet and got the result you see below. Note the strange look of the solution curve after t=0,021. If I set t.end to a higher value then 0,025, the solve block fails again with that "unknown error".
Remark: AS kg is the base unit, it may make more sense to set kg:=1 rather than 1000 as I did. Doesn't make much difference, though.
Disabling the "unit-definitions" at the top should work OK but for reasons unknown to me still doesn't.
I attach the Prime 6 worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The error message states a unit mismatch but we can't see the units you assigned to the various variables.
If possible you should attach your worksheet, not just a picture.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner,
Thanks for your fast response. I attached a version of my worksheet.
Alex
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You should delete the region saying "L:=0.1". After all L is not a variable but a function and you don't need a "guess" for a function.
I am getting a different error message -> "unknown error", not a unit mismatch ??
Nonetheless the solve block works OK if I delete all units (or set them all to 1).
So you may want to check your equations with respect to the units.
One additional remark: In the solve block odesolve command you set the end value for t to 0.001, but in your plot you try to plot up to t=0.8. That can't work.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your help.
I removed "L:=0.1" but still get a unit mismatch error. As in my description above, I believe that MathCAD has an issue since the ODE is non-linear and maybe requires a certain format to solve it. Due to it being non-linear, I think that the solver needs some sort of guess values.
Edit: Very interesting that it works when removing the units, I will play with this. Thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Obviously it has to do with the units and/or their magnitude.
I changed the values of the "unitless units" on top of the sheet and got the result you see below. Note the strange look of the solution curve after t=0,021. If I set t.end to a higher value then 0,025, the solve block fails again with that "unknown error".
Remark: AS kg is the base unit, it may make more sense to set kg:=1 rather than 1000 as I did. Doesn't make much difference, though.
Disabling the "unit-definitions" at the top should work OK but for reasons unknown to me still doesn't.
I attach the Prime 6 worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It was a unit error indeed, thanks Werner!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess the L(t) should yield a length (otherwise A1 would have to be a length and not be limitless).
If thats true, then L0 should not be mm/mm (meaning unitless) but just mm.
Furthermore you would have to delete the s/mm^2 at the end of your equation.
The inital condition should read L(0 s)= L0.. (note the unit s even if the value is 0)
If you do so, the equations should be OK concerning the units. Unfortunately the solve block still fails.
EDIT: The order of my replies seems to has changes. The last reply is above.