Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbolic Evaluation Variable Assignment Problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbolic Evaluation Variable Assignment Problem
Hi all,
I was seeing some strange inconsistencies between sheets when attempting to evaluate expressions symbolically. After some time I traced the inconsistency back to the "point" shown in the attached sheet.
The attached sheet shows what I expect to see. After evaluating a function and assigning the result to a variable, the symbolic evaluation shows the result.
However, in a different worksheet, I see the following:
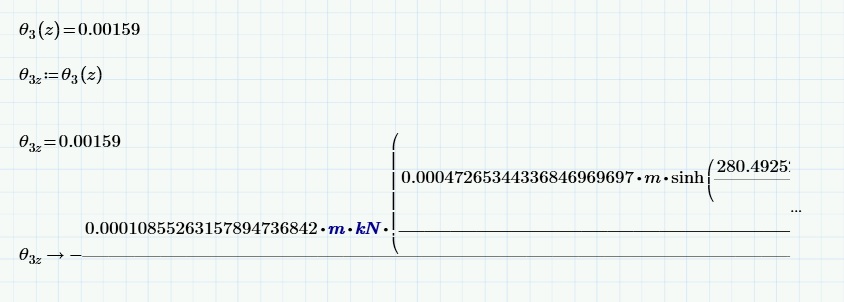
For some reason, Mathcad is presenting the result as the original function. I'll post the problem sheet if necessary, but as you can see here, Mathcad has already found a numeric solution and assigned it to a variable, and has even managed to display it when called up again. But when I use the symbolic evaluation on it, it brings up the whole function. But in the attached worksheet, it does not.
Any ideas why this happens? Or at least, why the difference between worksheets?
Any advice is greatly appreciated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Edward,
Please attach to the message your Mathcad Prime worksheet with the issue showen on screenshot above.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cannot read Mathcad Prime 3.1 ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Edward Plotkin wrote:
Hi all,
I was seeing some strange inconsistencies between sheets when attempting to evaluate expressions symbolically. After some time I traced the inconsistency back to the "point" shown in the attached sheet.
The attached sheet shows what I expect to see. After evaluating a function and assigning the result to a variable, the symbolic evaluation shows the result.
However, in a different worksheet, I see the following:
For some reason, Mathcad is presenting the result as the original function. I'll post the problem sheet if necessary, but as you can see here, Mathcad has already found a numeric solution and assigned it to a variable, and has even managed to display it when called up again. But when I use the symbolic evaluation on it, it brings up the whole function. But in the attached worksheet, it does not.
Any ideas why this happens? Or at least, why the difference between worksheets?
Any advice is greatly appreciated.
What you're seeing is expected behaviour and is the result of the symbolic processor not being designed to handle units. As far as symbolics are concerned, units are just names and have no special meaning. Furthermore, they have no value, so the symbolic processor does what its name suggests and simply evaluates them as symbols. This will consist of basic simplification (eg, m/m = 1) until it can't reduce the expression anymore. If you were to define all of the units (in Unit Label) as 1, or the appropriate multiple, you'd get a pure numeric answer from the symbolic processor.
Try typing x:=1 m and then symbolically evaluate x. It would be more obvious what was going on if the symbolic processor retained the Math Label.
If you type = in line with the symbolic evaluation, you will also get a correct numeric answer as the symbolic processor passes the expression to the numeric processor (which is units aware) before assigning the result to the variable.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But how come in the sheet which is attached in my original post, it works fine? It still has the same units (I think, I'll have to check when I'm at work again). Why the difference between the two sheets?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Edward Plotkin wrote:
But how come in the sheet which is attached in my original post, it works fine? It still has the same units (I think, I'll have to check when I'm at work again). Why the difference between the two sheets?
Your units cancel (symbolically) in the first sheet, so you get a pure numeric result. They don't cancel in the second sheet, so you get the symbolic result. Try defining GPa:=1 at the start of the first sheet and you'll see that you get a result in Pa from the symbolic processor.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I must admit I am still skeptical. I have the same units in both cases. The only major difference between the two sheets is in the one that behaves as expected, the variables are assigned directly, by me. In the other case, they are worked out over a number of calculation steps.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Edward Plotkin wrote:
I must admit I am still skeptical. I have the same units in both cases. The only major difference between the two sheets is in the one that behaves as expected, the variables are assigned directly, by me. In the other case, they are worked out over a number of calculation steps.
Annnddd ... I think you're quite right to be sceptical! When I first looked at your problem, I wondered if there was some issue with Prime knowing that trig functions take radian measure and slapping in a m/m unit somewhere along the line. However, this turns out not to be the case as it happens even with plain arithmetic operations.
Here's what M15 M040 has to say about a simplified version of your problem:

And here's what Prime 3.1 thinks:

So it looks as though there is problem with the mm to m conversion. The interesting thing, for me, is that the symbolic processor is more unit aware than I thought it was - I avoid units if I possibly can because, historically, they created more problems for me than they solved.
However, a little more playing around and it looks like the inline conversion is at least partially implicated, although it doesn't explain the above.

Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
On the other hand, there is an option in Calculation ribbon for dealing with Units or Constants in symbolics ...
There's a section in Help about it: About Units and Constants in Symbolics
Stuart

From Help
The default label styles of inserted units and constants, as well as typed-in variables, are as follows:
|
Labels that are assigned by the system, or explicitly by the user, to an identifier do not change with context. Examples of such labels are ones that are set by default in the unit or constant placeholders or set by default when solving functions are inserted and so forth.
As a PTC Mathcad user, you have control over the assignment, and reassignment, of labels and label styles. This is true both when you perform symbolic or numeric calculations.
You can enable the Units/Constants in Symbolics option to give PTC Mathcad some control over the assignment of labels and label styles. In this PTC Mathcad infers the label and returns it as part of the result of a calculation.
Note
|
This is the default state when you open a new worksheet. Here, you have control over assigning labels to typed-in identifiers. In this case:
- Inserting a unit from the Ribbon gives the unit the label, and label style, of Unit. Evaluating the unit symbolically results in the right-hand-side (RHS) of the equation also getting assigned the label, and label style, of Unit.
- Inserting a constant from the Ribbon gives the constant the label, and label style, of Constant. Evaluating the constant symbolically results in the RHS of the equation also getting assigned the label, and label style, of Constant.
- Manually typing in an identifier gives the identifier the label, and label style, of None. Evaluating the identifier symbolically results in the RHS of the equation also getting assigned the label, and label style, of None.Example:
- Type the expression m +. PTC Mathcad assigns m the None label.
- Type a second m and manually assign it the Unit label
- Symbolically evaluate the expression:

In this case, the result is identical to the input expression because PTC Mathcad does not attempt to resolve the labels based on its knowledge of built-in units or constants. PTC Mathcad treats the seemingly identical variables differently because they are labeled differently.
NoteIn general, if you type an identifier that has no special meaning to PTC Mathcad – a unit or a constant – then the identifier gets the default label of None. An exception to this rule applies when manually typing in the identifiers ∞ (Ctrl+Shift+Z), e, or π (p, Ctrl+G):
- Identifier ∞ is assigned the label, and label style, of Constant immediately and before applying the symbolic evaluation. After evaluation, the result is also assigned the label, and label style, of Constant.
- Identifiers e and π are initially assigned the label, and label style, of None. After evaluation, the label of the LHS remains None, but its label style changes to Constant. The results are assigned the label, and label style, of Constant.
By enabling this option you allow PTC Mathcad to resolve and assign labels based on its knowledge of built-in units or constants.
Note If you enable this option after symbolically evaluating the previous expression, then PTC Mathcad returns:
The labels of the left-hand-side (LHS) remain unchanged, but their label style changes to Unit. However, the labels, and label styles, of RHS change to Unit. This allows PTC Mathcad to symbolically add two variables that have the same label. |
The insertion of units, or constants, from the Ribbon followed by symbolic evaluation yields the same results and labels as before. Thus, enabling this option has no effect on the built-in units and constants.
However, manually typing in identifiers and evaluating them symbolically yields the same results but the assigned label, and label style, depend on what you manually type-in:
- Typing an identifier that PTC Mathcad does not recognize as a built-in unit or constant, such as x, and evaluating it symbolically results in PTC Mathcad assigning both sides of the equation the label, and label style, of None.
- Typing, but without evaluating, an identifier that PTC Mathcad recognizes as a built-in unit or constant, such as c or m:
- PTC Mathcad assigns it the label, and label style, of None.
- If the typed identifier is c, then symbolic evaluation results in the LHS keeping the None label and PTC Mathcad automatically assigning the LHS the label style of a constant and assigns the RHS the Constant label and label style.
- If the typed identifier is m, then symbolic evaluation results in the LHS keeping the None label and PTC Mathcad automatically assigning the LHS the label style of a unit and assigns the RHS the Unit label and label style.
Note PTC Mathcad always treats ∞, e, or π as if the Units/Constants in Symbolics option is enabled. |