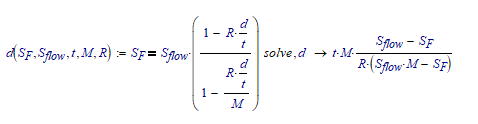Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Vector Solve Block Simple Equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vector Solve Block Simple Equation
Hi,
I am really new to Mathcad.
I have a problem to find a "d" variable in constraint with L as the dependent factor. The problem is, I want to get "d" with range variables of L from 0 to 1000 mm. So I get range value of "d" based on the L inputs.
Could we do this by that way with solve block? Appreciate your guy's help
- Labels:
-
Mechanical_Engineering
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
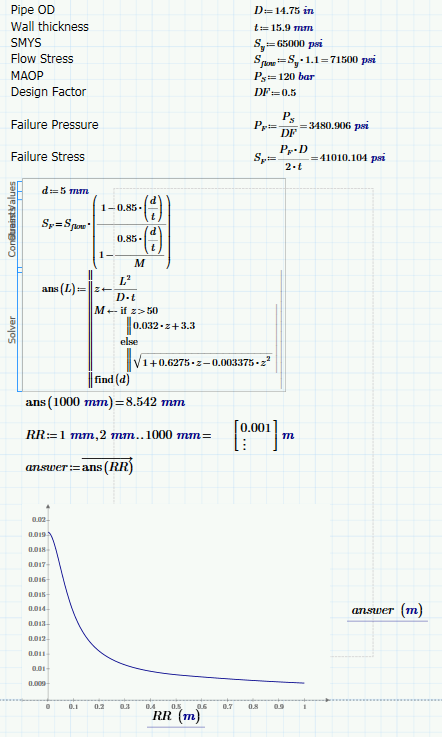
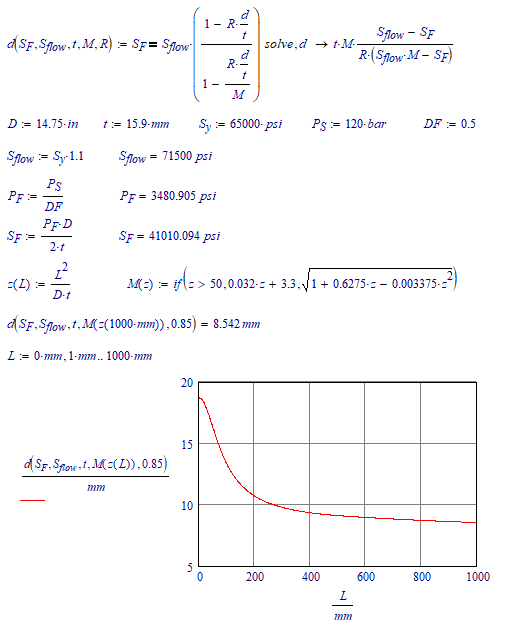
Yes, you could. But I think it's much simpler if you first solve, like this:
That is, you define a function d, where the definition uses a symbolic solve. That 'll get you best accuracy, and speed.
In your case, R=0.85.
Now if you make M a function of z, and z a function of L, D and t, you can call:
d(S.F,S.flow,t,M(z(L,D,t)),0.85)=...
And you can plot d(...) versus L.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Along the same line of thinking paramatise the solve block in terms of L
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
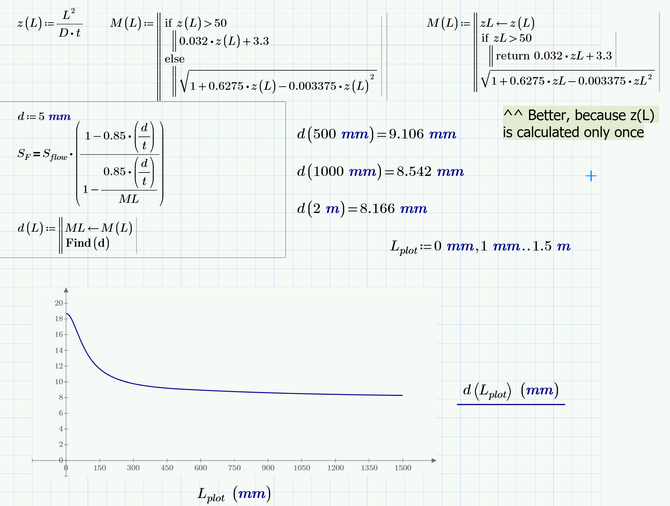
I did mine the way I did as I believe it's faster. As I understand things, once mathcad starts iterating it will call M(L), and hence z(L), for each iteration. Not a big deal here, but it can slow things down in big programs. Also the solver isn't terribly robust imho and gets confused with 'constants' inside of a solve block. I've found the 'program' internal to the solve block to be very effective. But that's probably more than our poster needs to know at this point.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the hints DJF
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks DJF, it is also another way of thinking that solve my problem as well.
Cheers!!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In other words, simply like this:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You made my day simpler. Really appreciate it
Thanks,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a way which follows closely your approach and still avoids multiple calculation of M(L) during iterations:
But I agree with Luc that in case of your rather simple equation it would be better to solve it symbolically and go for the most direct approach:
Worksheet in Format Prime5 attached