Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Vector solve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vector solve
Hi,
It is not the first time I want to find solutions to the same equations with different parameters/inputs, but it is the first time I do with more than 2 or 3 (I usually just did copy and paste). So for the first time, I am really trying to get Mathcad to solve equations with vectors on the input and output (but all scalar operations).
With what I did, Mathcad doesn't show any error, but the outputs are equal to the guess values, which seem to indicate that it doesn't work.
Practically, I have a circuit with a RL series with another R in parallel (R // (R - L)). I have measured it at different frequencies, measured the impedance and phase angle, and I want to identify the unknown parameters (series R L ). All parameters may vary with frequency (in fact, they probably do !).
Thanks
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Adrien,
First of all, it looks as though the equation for impedance is not correct. Your Rp does not have units. I appended kilo-ohms to Rp, but got a units error for Zz. Using symbolic evaluation, I obtained an equation for impedance that differs from yours, but the units match.
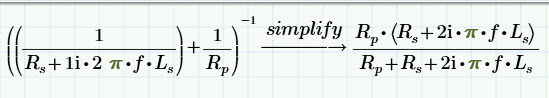
After that, I removed the vectorize operator from the constraints and instead put them over each side of the constraint equation. When the vectorize operator is applied to the entire constraint equation, the solve block does not recognize it as a constraint. Instead, you need to calculate, one-by-one, each side of the constraint equation and compare one-by-one.
Now, what I have attached gives results that, when plugged back into the constraint equations (switch to draft view to see the verification), adhere to the constraints. In other words, the solutions are valid numerically, but you'll notice that the resistances show negative values, which is not valid physically. Therefore, you can add an additional constraint of Rs>0, but then the find function does not converge to a solution.
I tried appending ohms to Rp instead of kilo-ohms, but this did not seem to work either. So now the solve block is working, as I believe you desire it to, but something in the constraint equations or the given values does not seem to be correct (maybe I incorrectly solved for the impedance equation).
Hope this gets you on the right track.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Adrien,
First of all, it looks as though the equation for impedance is not correct. Your Rp does not have units. I appended kilo-ohms to Rp, but got a units error for Zz. Using symbolic evaluation, I obtained an equation for impedance that differs from yours, but the units match.
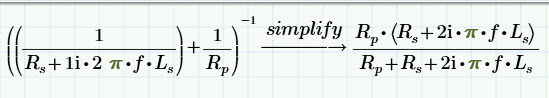
After that, I removed the vectorize operator from the constraints and instead put them over each side of the constraint equation. When the vectorize operator is applied to the entire constraint equation, the solve block does not recognize it as a constraint. Instead, you need to calculate, one-by-one, each side of the constraint equation and compare one-by-one.
Now, what I have attached gives results that, when plugged back into the constraint equations (switch to draft view to see the verification), adhere to the constraints. In other words, the solutions are valid numerically, but you'll notice that the resistances show negative values, which is not valid physically. Therefore, you can add an additional constraint of Rs>0, but then the find function does not converge to a solution.
I tried appending ohms to Rp instead of kilo-ohms, but this did not seem to work either. So now the solve block is working, as I believe you desire it to, but something in the constraint equations or the given values does not seem to be correct (maybe I incorrectly solved for the impedance equation).
Hope this gets you on the right track.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can't use a solve block that way. If you have multiple cases to solve for you have to turn the solve block into a function, and then apply the function to the multiple cases.
You have a more fundamental problem though. In the function Zz the units in the numerator and denominator are fundamentally incompatible. The numerator requires that Rp be unitless, whereas the denominator requires that Rp have the units of Ohms. So first, you need to fix the formula for Zz.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can't use a solve block that way.
Why not? I think that Jonathan had worked out a solution which works pretty well and followed the vectorial approach, Adrien had tried to use.
Nevertheless I, too, prefer to set up the solve block to work with scalars, turn it into a function which then is called vectorized. Its a bit more work to separate the results when we do it that way, though. I have done it and got the very same results as Jonathan. When Rp is assigned the unit Mohm, we even get postive solutions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yeah, I guess. If you set it up right it just sees a large number of equations with a large number of unknowns. IMO setting it up that way is very confusing though, because it makes the problem look much more complicated than it actually is. It's also very inefficient, because the computation time for an iterative least squares solver goes as the square of the number of unknowns.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's also very inefficient, because the computation time for an iterative least squares solver goes as the square of the number of unknowns.
Thats sure a very good point!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much ! Both solution are great ! I am particularly surprised by the "solve function", I never thought that would be possible (and it opens a new range of possibilities).
Thanks !
Jonathan, regarding the weird values as result ... I am having a lot of trouble with that, but it is down to my model, not to Mathcad ![]()
Basically, I want to characterise an inductance, including losses caused by the fringing field and proximity effect. I consider my inductance as a (Rs -L) // Rp, Rs being the losses in the windings, Rp losses in the core. Due to variation of permeability with material, core losses variation with B field and frequency, fringing field, etc, all parameters vary with frequency. Rp I got from calculating the core losses, frequency, impedance and phase I measured on my inductance. Presently, Rp is calculated from the characteristics of the wrong core material, but I will change that soon. That may cause some weird values, but it is not the worst. Currently, if I extrapolate the losses due to the fringing filed (by finding the best fit for Rs(f)), my losses diverge. Which is kind of a big issue...
Anyway, whether I manage to make sense of my model or not, I have learnt new things today thanks to you, and that's great !


