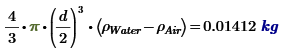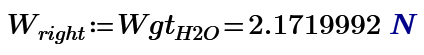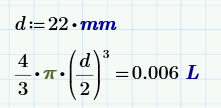Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Water, Air, Steel
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is an intriguing problem, that forces one to think about how to apply Newton's laws in a basic way. Here's my take on the problem.
First, I will assume the masses of the string, beaker, balloon, etc, are all zero. They do not add anything to the basic structure of the problem, and can only add unnecessary complication. Also, the nature of the problem is such that which side of the scale has the most force on it can be determined without any calculations in the idealized case.
Consider the issue of buoyancy and the left side beaker. The water exerts an upward buoyant force Fb on the balloon (which has air in it, but not necessarily). By Newton's third law, the buoyancy creates an equal an opposite force on the bottom of the beaker, so that for the combined beaker, water, air balloon, string system, the net downward force remains the weight of the water plus the weight of the air.
One way to see this is to do the following thought experiment: consider the net downward force on the scale if there is water in the balloon. There is still an upward buoyancy force Fb on the balloon, which in this case is exactly nullified by the weight of the water in the balloon. If we don't take the reactive downward force of the buoyancy on the bottom of the beaker into account, then the net effect of the buoyancy is to negate the weight of the water in the balloon. This is clearly a nonsensical result.
Since there is water both inside and outside the balloon, the net effect is that the balloon has no effect, and can be disregarded. Clearly, the total weight of the system - the force on the scale - is the combined weight of the water inside the balloon and the water outside the balloon, which is the answer we get by considering the buoyancy to also be a reactive force downward on the bottom of the beaker (and the scale).
As a consequence, the total weight - downward force - on the left side of the scale is the weight of the water plus the weight of the air. This is also the result by isolating the beaker, water, air, balloon system. Except for the gravitational weights of the air and water, all other forces are internal to the isolated system, and thus have no effect of the overall downward force.
For the system on the right, we may replace the steel ball and string with a rigid support and a ball of arbitrary material - heavier of lighter than water. the rigid support will be in tension or compression depending on whether the balloon material is heavier or lighter than water. In this case as before, the buoyancy has no net effect on the downward force against the scale. However, the external support provides the counter-force to the weight of the material inside the balloon. Hence, the net downward force on the right side scale is just the weight of the water outside the balloon.
The force on the left side scale being greater, the left side will go down (assuming the left balloon does not contain a vacuum, in which case the scale will balance).
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
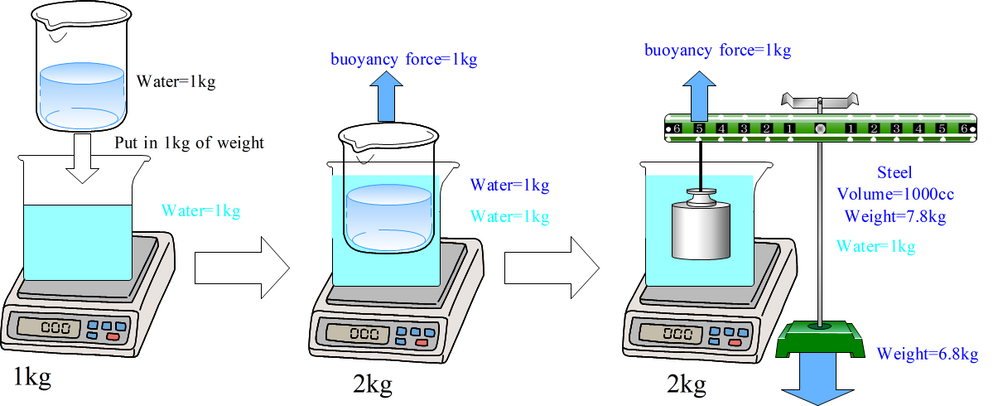
Left side.
Air in beaker also affected by the buoyancy force by air.
Therefore, the weight is zero.
Right side.
The buoyancy force of the sphere volume of water increases the weight of beaker when the outside of sphere filled in the water in beaker.
This counter force decreases the weight of steel ball measured at outside of scale.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
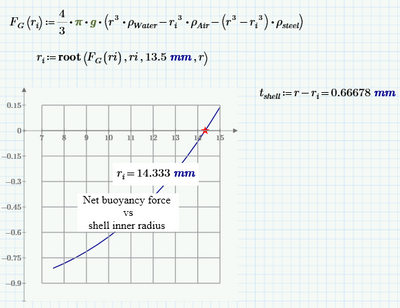
I ask the students a new problem after analyzing the old one - what should be the thickness of the steel wall of the spherical shell in the left glass for the balance to be balanced! H, D and d are given! With plot DeltaG:=f(thickness).
The best Physic hand book for high school
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Per your request:
Extended analysis attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I tried to break this down as simply as possible, but it's very tricky.
See if this enlightens or confuses.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred could you also provide a pdf of your analysis? Thank you
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I still have a problem with the analysis that says the left side is lighter than the right side. Somehow, the weight of the air is not adding to the net force on the scale. since the beaker, string, water and air are an enclosed system (no external support except for the scale platform), any forces acting within the beaker must cancel, except for the gravitational weight of the masses - air and water in this case. From this viewpoint, the net weight on the scale platform must be the combined weight of the air and water, which is already heavier than the net weight on the right, which all seem to agree is due to the weight of the water only.
My issue is the treatment of the buoyancy force. Consider the spherical shell to be rigid and massless; likewise for the string, so that it can support compression as well as tension. Regardless of the content of the spherical shell, there is an upward buoyant force on the shell equal to the weight of the displaced water. By Newton's second law, this force must have an equal and opposite reactive force. In this case, it is a downward force acting on the bottom of the beaker. This component is ignored in the analysis, resulting in what I believe is an incorrect conclusion.
To see why this must be so, consider the following thought experiment. Let the sphere contain water instead of air. In this case, the upward buoyancy force on the sphere will exactly counter the weight of the water in the sphere, resulting in zero tension in the string. Following Fred's analysis, the left rod force will now be zero, instead of +0.138 N. The Fleft force is now equal to the water weight outside the sphere. This is clearly a nonsensical result, since the sphere and string can be removed without changing anything (no forces on them), and the total weight on the scale must include the weight of the water within the sphere as well as outside it.
If the buoyancy force is envisioned as a compressed spring between the bottom of the water (inside surface of the beaker) ans the spherical shell, then the upward force on the shell also results on a downward force on the beaker, and everything works out well. Doing this for the left side restores the mass of the air as a net downward force, as I believe it should be.
If this is correct - as I believe - then increasing the weight of the spherical shell will only increase the unbalance.
What do you think? Is there an error in my analysis?
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Lou,
Rather than calculate weights, work with pressures.
Attached is a point-by-point discussion. (Your analysis on the left is correct (pressure and weight calculations agree) but the right has a surprise. (The right sphere raises the pressure head on the bottom of the beaker.)
Attached is Prime 4, and a pdf
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Without going into a detailed analysis of the various forces, and which ones may or may not have been left out, let me offer the following thought experiment. Consider two identical beakers, one with a vacuum filled volume in it (may be a sphere or otherwise, as in our examples), and one with no occupied volume. Again, to idealize the situation, consider the spherical shell and its support to be massless, so the two beakers have identical weights.. Now put identical masses of water into each beaker. The resultant water level in the beaker with the vacuum sphere will certainly be higher than the one without this volume displacing sphere. The bottom pressure on the beaker with the sphere, having a larger water depth, should be be higher than the pressure at the bottom of the other beaker. Now my question: do you believe that the net force on the scale is different for the two beakers, even though an identical mass of water was added to each beaker? If you do, then you must believe that the shape of the vessel has an impact on the net weight of the scale. Note that the assuming that the net downward force on the beaker is due solely to the water pressure ignores any force on the bottom due to the string (or sphere support).
As a simple example, consider two beakers with different diameters. Putting equal masses of water into each will result in different water heights. I don't think this would affect their net weight on a scale. In this case, the larger pressure at the bottom will be exactly compensated by the smaller area, resulting in the same net force on the beaker bottom.
In the case of the internal sphere - or for a simpler analysis, consider a cylinder - I believe that a careful analysis of the forces on the top and bottom of the cylinder, combine with other forces due to pressure at the beaker bottom, will result in a net force equal to the total weight of the water, regardless of the details of the geometry. This must be the case based on very basic considerations. If the detailed calculations don't agree, then I think the calcs are missing something - not the general principle.
Again, I don't think that detailed calcs are necessary; only a description of what the various force components are, and whether they cancel.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
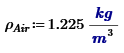
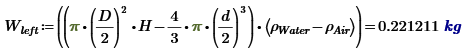
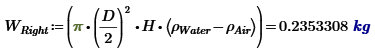
So the right is heavier than the left by the weight of the water in the sphere.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Lou,
I can't dispute your logic.
But there's an experiment that I think might shed some light on the question.
We need:
- a measuring scale
- a beaker
- an accurate volume measurement
- a block of material (heavier than water) that fits inside the beaker and has a volume slightly less than half of the beaker.
Step One:
- put the block on the scale, put the beaker with water on top of the block.
- Read and record the scale reported weight.
Step Two:
- Put the beaker with water on the scale, put the block in the beaker. (Don't spill the water!)
- Read and record the scale reported weight.
Will the two measured weights be the same?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, Fred. The weights must be the same because in step 1 and in step 2 you're putting the very same mass on the scale.
Regarding the original problem, as posed by Valery:
After some more thought I'll stick to my last conclusion (see above, 2020-08-14 10:48 PM), the scale is in balance.
Note that the apparatus put up by Valery is a mass balance. It works on the principle that the gravitation field strength on whatever mass is on either scale is the same for both sides. Thus if equal masses are put on the two scales, gravitation will pul with the same strength on either side. That, and ONLY that will mean that the (downward) forces on both scales are equal. Further assumptions are that:
-The water is superfluid, so it does not exert any 'glueing' force on either ball suspended in it.
-The temperatures on either side are the same.
-The beakers are perfectly identical and all shapes of solid material of the mass balance and the stand are rigid (not compressible/expandable).
- The mass balance is ideal (perfectly symmetric and frictionless).
-The air in the ball in the left beaker is the same as the air outside (same temperature, same pressure).
Now note that the steel ball is fully supported by the stand, so it does not count to the mass on the right scale. Essentially the steel ball creates a vacuum in the right beaker because it is supported by the stand.
On the left side, the ball of air contains the same air as the air outside the water. So it will not sink, nor float to the top of the surrounding air, when allowed to escape. This means that the ball of air also does not put any mass on the left scale. So essentially the air ball in the left beaker creates a vacuum because it is supported by the surrounding air (this is what took me most of the time)
Then the only masses on both scales are the beakers and the amounts of water. Those being equal on either side, means that the scales balance perfectly.
We've all been puzzling about this for days; my daughter figured it out within 5 minutes.😦
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
If you look at the response I just posted to LouP, you'll see that I agree (and demonstrate) that the scales do agree.
Val's problem is different, however, because of the external support!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Still you have an error in right side. Include the weight of sphere volume of water for right side.
This value is same as the buoyancy force.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
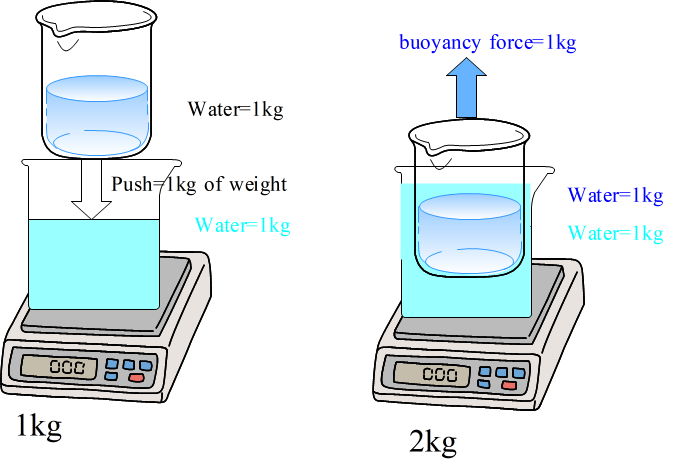
Nice graphics!
Are you saying (on the left) that if I put two beakers, each containing 1 kg of water, side by side on a scale (you've shown them on top of each other) that the scale will report 1 kg?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting question.
Large beaker has no cap on the top. Therefore, small beaker is hold over the large beaker by someone.
So the weight of large beaker is 1kg.
You understand after put into the small beaker to the large beaker, the total weight is 2kg.
By the way, steel ball immersed in the right side beaker has the buoyancy force and it is same if the steel ball has external support or has not.
I want to know your final answer for the original question.
Right side -- kg. Left side --kg.
Tokoro.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Our fun discussion of this puzzle.
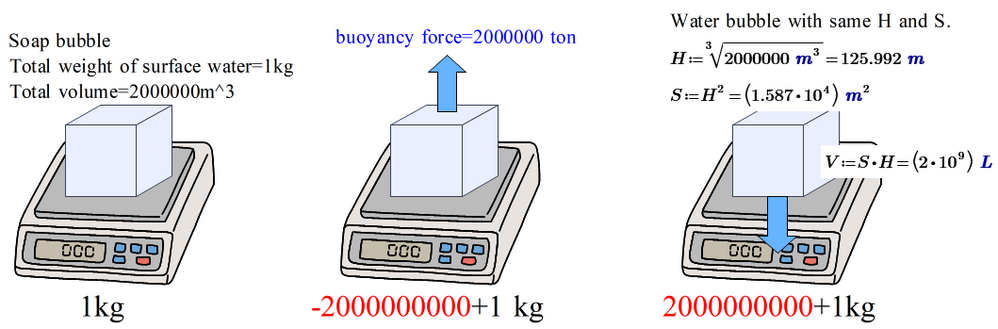
Weight: 1kg or 1kg-2000000 tons or 200000 tons + 1kg?
Nature knows the answer.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
On the left side, the ball of air contains the same air as the air outside the water. So it will not sink, nor float to the top of the surrounding air, when allowed to escape.
Really? Does Archimedes know this? Try it in your kitchen sink with a tupperware container (a watertight container that will not collapse when submerged.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No, Fred, read carefully:
In my kitchen a ball of air will not sink to the floor, nor float to the ceiling when released to the free air in the kitchen.
Maybe I should have written: "when allowed to escape from the water it is contained in".
My point is: the air entrapped in the water column exerts no force on the surroundings, so it could be sitting inside the water, or on top of it (in which case the upper level of water would go down because now the volume that the air occupied becomes filled with water), or the air could be entrapped on the bottom of the beaker (by some means).
In essence this means that you cannot determine the mass of a volume of air by using such a mass balance ..........
Hmmm. Forget about the water, and the beakers. What happens if I attach only a ball to each of the two scales? The left ball, tied to the left scale is filled with the same air that surrounds it. The other ball tied to the right scale contains a perfect vacuum.
Of course the balls are perfectly identical; as well as the ropes that tie them to the scales; OK, for sake of simplicity make them massless..
It's still an intriguing problem.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No, Fred, read carefully:
Always a problem with me! 😉
In my kitchen a ball of air will not sink to the floor, nor float to the ceiling when released to the free air in the kitchen.
Yep! Same here. Sorry for not reading carefully.
In essence this means that you cannot determine the mass of a volume of air by using such a mass balance ..........
Well . . .
Archimedes' Principle says that the buoyancy force equals the weight of the water displaced. But the net force (weight) of a submerged object is the buoyancy force minus the weight of the object. That's how we decide whether a boat floats or sinks--if it weighs more than the water it displaces the boat sinks. Doesn't this mean that we can weigh the air in the sphere if we're crafty? (I haven't figured out exactly how yet. . .)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Q. E. D.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Lou,
A second look at your latest comments.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I’m having a hard time keeping the various responses separate, and which problem is being addressed in the response. Below is a revision of my response to the Val’s original problem. I had ignored the fact that the beakers are in atmospheric air, rather than a vacuum. Looking to simplify things, I ignored the air, and presented the problem as if it were in a vacuum. (I think that my analysis that the left scale would indicate heavier on the scale is correct with this assumption.)
In air, there are additional considerations. Let me number my assumptions and conclusions to make responses a bit easier.
1. The string and steel ball on the right side are red herrings (distractions). Since the only parts of the system supported by the scale are the beaker and its water, these are the only relevant items when analyzing the scale force of the right side. Forces on the steel sphere/support are supported by the structures outside the beaker/scale system.
2. I stand by my analysis of the left side which says that the component of downward force on the scale from mass in the beaker/water/sphere system on the left is just the combined weight of these masses, which - idealized - is the weight of the air in the sphere plus the weight of the water. The buoyancy of the sphere within the water Is an internal consideration, and can be ignored (more accurately, has cancelling forces) when considering the weight of the beaker system mass.
3. What was ignored in my original analysis Is the buoyancy of the beaker system in the air surrounding the system. (This argument presents another chain of reasoning supporting the argument by Luc, and his daughter, which says that the air in the sphere has zero net effect on the scale reading.)
The beaker system in air has a certain buoyancy. This is normally 3-4 orders of magnitude below the weights of everyday liquids and solids. In this case, let’s not ignore it. On the right side, the upward force component due to the buoyancy of the system in air (remember just the beaker and water, not the steel) is the weight of the air displaced by the beaker and water. On the left side the buoyancy of the system in air is the weight of the air displaced by the beaker/water/sphere; somewhat larger. If the air density in the sphere equals the density of the surrounding air, then the weight of the air in the sphere will exactly cancel the additional buoyancy due to the additional displacement volume of the sphere. Then the net downward force on the scale is the weight of the water less the buoyancy- in air - of the water volume. This is identical to the net downward force on the right side, so the scale balances.
4. Now, addressing Luc’s problem of the air sphere on one side and a vacuum sphere on the other side. On both sides, the water weight is the same, as is the buoyancy of the two sides in the surrounding air (same displaced volumes). Since the side with the air sphere has higher mass, and weight, the air side will weigh more on the scale, and lower the scale on that side.
I think I finally have things sorted out where I understand what is going on. Please let me know if I’ve gone astray somewhere.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Mathcad users,
Please show your final decision.
This is a principle, a fundamental truth, the answer is only one.
Tokoro.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks.
A spring scale measures weight, by seeing how much the object pushes on a spring (inside the device).
Therefore, the left side measures
Is the right side measures
or

Which value does the spring scale show?
Tokoro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I decided to do an experiment to see what's going on at the right side.
I filled a glass with some water and put it on the kitchen weigher, then set the scale to 0.
This is what you see here.
Then I took a ball (from a computer-mouse), tied to a fishing-string and suspended it in the water. I expected the weigher to keep indicating 0, instead it showed:
So the weight actually increases. I did the same experiment but pressing a measuring cup into the water. (You actually have to press it in, because it wants to float; that's something you don't experience wth the steel ball. This is what, up to now, had sent my thoughts the wrong way). The increase in measured weight was consistent with the scale on the measuring cup. The increase in weight is the weight of the displaced water.
So I must correct my analysis. The right side, with the steel ball suspended to the stand, weighs the height of the water, as if it were all water. Oh, my ball weighs 30 g, and it measures 22 mm in diameter:
There's my 0.006 L, in water that's 6 g.
So the right side of the balance carries a weight of the outer volume of the water, which is
Now I have to figure out a way to measure the left side phenomenon.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
百聞不如一見
百見不如一考
百考不如一行 Now we are coming here!
百行不如一効
百効不如一幸
百幸不如一皇
Buoyancy force is same for the same volume. It is same when the sphere material is Air, or the one is Water or even the one is Steel.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is my one line:
Luc