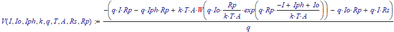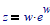- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
genfit() to solve for nonlinear parameters
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
genfit() to solve for nonlinear parameters
How to use genfit() to solve for nonlinear parameters since it is hard to separate I or V from the equation?
- Labels:
-
Mathcad Usage
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
genfit will not fit a function of two variables?
You need six constants to solve the problem.
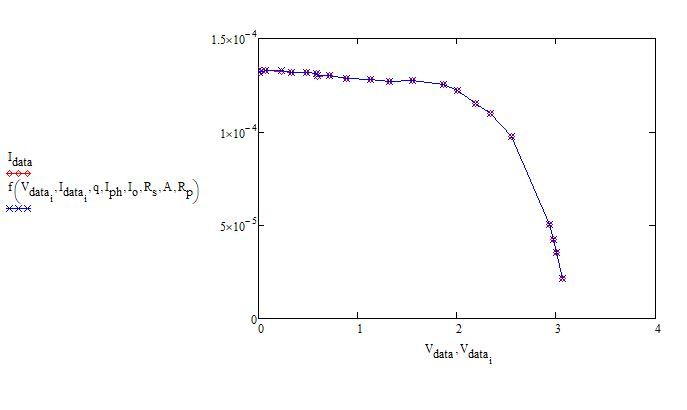
Here is a solve block that gets close.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
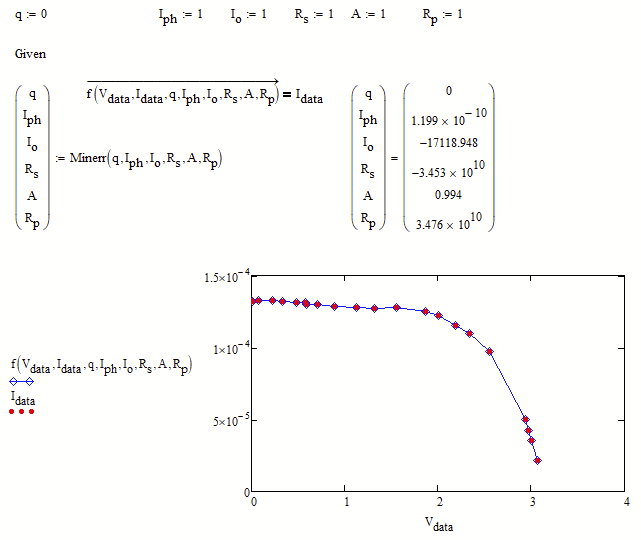
Why not consider ALL data and use "minerr" instead of "find":
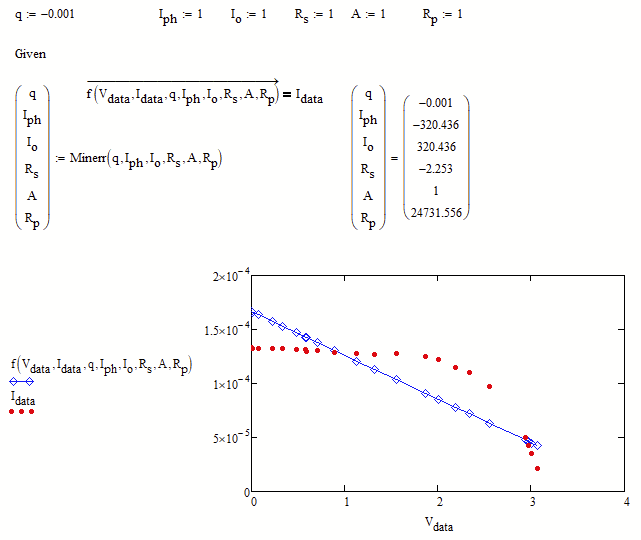
But the result is only satisfactory if the guess for q (which does not seem to be changed by the solve block) is set to 0:
The whole thing is quite dependent on the guess values - as an example try changing the guess for A and look how the other values change.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In this equation you cannot choose the value of q freely. It's value should be the electron charge (while k is the Boltzmann constant, and T is the absolute temperature). It makes that k*T/q is about 25 mV.
Note that you can write V as an explicit function of I and the other parameters:
Or, in other words:
where W is the LambertW function (relation).
The LambertW(z) function is the solution of w, with given z to the problem:
It is (only symbolically) available in Mathcad 15. Attached is a Mathcad 11 sheet with a numeric approximation of the function. I hope it works in 15.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For completeness sake here is solution with q set to electronic charge value.
You can use genfit() with Luke's formula.
Cheers
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can use genfit() with Luke's formula.
Not out of the box! The LambertW function in MC15 is a symbolic only function and can't be used with genfit. However, one should find numerically evaluable implementations of the LambertW function in some older threads here in the forum, if that should be the desired way to go.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Io should not be 0, that shuts down the diode. And the resistor values Rs and Rp should both be positive and not in the TeraOhm range. Finally A is expected to be in the range 1 to 2. A=1 implements an ideal diode.
Luc