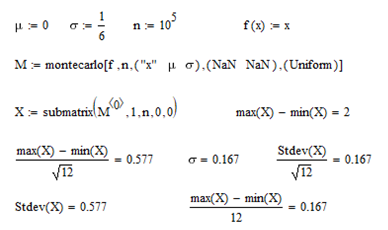- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
sensitivity analysis in equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
sensitivity analysis in equation
Hello,
can I perform a sensitivity analysis with Mathcad Prime 4.0? As a result I would like to know which parameter has the greatest effect on the Output. There are local and global sensitivity analysis. At local sensitivities, only one parameter is varied and all others are kept constant. Globals also indicate the interaction between the Parameters. Or maybe there is another oppurtunity.
Thank you
Solved! Go to Solution.
- Labels:
-
Programming
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
With the exception of the Uniform distribution issue I mentioned earlier, it looks to be working fine. M truly dominates the equation with its large variance. Or else point me to a specific issue you're seeing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@s-soberh wrote:
Hello,
can I perform a sensitivity analysis with Mathcad Prime 4.0?
Guess yes, but not out of the box. It looks like it would require some programming in Prime.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are multiple ways it could be done.
a.) programming as Werner suggests. Perhaps the most robust of the solutions
b.) Redefine one variable at a time as a random vector (runif works well) and vectorize any equations as necessary
c.) built in montecarlo function. You can change each variable's standard deviation individually. Make stddev zero for all but one variable and see how the output changes for each one.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe something like this
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Based on your message, I tried it with the Monte Carlo. Unfortunately, I do not know how to continue. Maybe someone has the time and the desire to look at it. It would be great if you could write down the necessary lines. Best with a graph, which parameter has the most influence.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Easy enough, you just have to replace the relevant input data in my sheet. Unless you want something different.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many Thanks DJF for your quick support.
I would have made a small change, but the values in the graphs do not match the means and standard deviations. I've added two more parameters, but it looks like it's not working anymore, although in my opinion I've changed everything.
Do I have to change anything in the program?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No time to look at it right now, but note the uniform distribution is tricky. Add lower and upper limits for it.(or switch to normal) By default it goes +/- 6 (a six sigma thing?). The deviation typed in has an effect on this, but needs to be quite small. So leaving that big and defining the limits works best. (There is a std dev mathematical definition for a uniform distribution, but it sure doesn't work here. So I've never really figured out what mathcad is doing).
I'm hoping Werner can explain it. 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner,
Can you?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I read it, but am unsure which effect or bug needs explanation. Would need an example.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The question is about how Mathcad uses the uniform distribution within the montecarlo built-in function. The input is the distribution (Uniform) and a standard deviation (and optional limits). (maybe std dev is the wrong term here, but it goes in the same column as the other std devs) The distribution responds to the deviation input typed (i.e. upper and lower limits move), but I'm stumped as to what the mathematical relationship actually is. So I just set the optional hard limits and I seem to get a distribution that looks appropriate - but without understanding the math maybe I'm doing something wrong. Seems like the kind of thing you're normally knowledgeable about. For examples just see my files in this thread - 3rd row in the inputs. Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, I never used the built-in Montecarlo function so I am lacking the experience here.
From the syntax in he help it looks that you will have to provide the limits-vector anyway unless all variables are normal distributed. Or does the function recognize the dist vector correctly even when the limits matrix is not provided?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, I played around with montecarlo and the uniform distribution and here is what a found:
If a and b are lower and upper limit of the uniform distribution, the standard deviation is sigma=(b-a)/sqrt(12).
Someone at PTC might have made an mistake as the value of sigma in montecarlo is interpreted simply as (b-a)/12.
So, if you want a uniform distribution with limits [3;5] you would provide mean value mu=4 and (the wrong) standard deviation sigma=1/6 (the true standard deviation of this distribution is 1/sqrt 3 ).
This strange effect is also present in Mathcad 15 (which is the version where DOE and montecarlo were introduced the first time if I remember correct).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
With the exception of the Uniform distribution issue I mentioned earlier, it looks to be working fine. M truly dominates the equation with its large variance. Or else point me to a specific issue you're seeing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
An improved version with an excel graph.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime is very proud of their "Design of Experiments" functions. There is a function "effects" that looks like it might do what you're looking for (if you can figure out how to apply it.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
DOE is also implemented in real Mathcad.
Maybe this doc can help additionally to understand how to set it up
http://gekor-it.de/media/442a9e0d3eafb80effff806bfffffff4.pdf
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
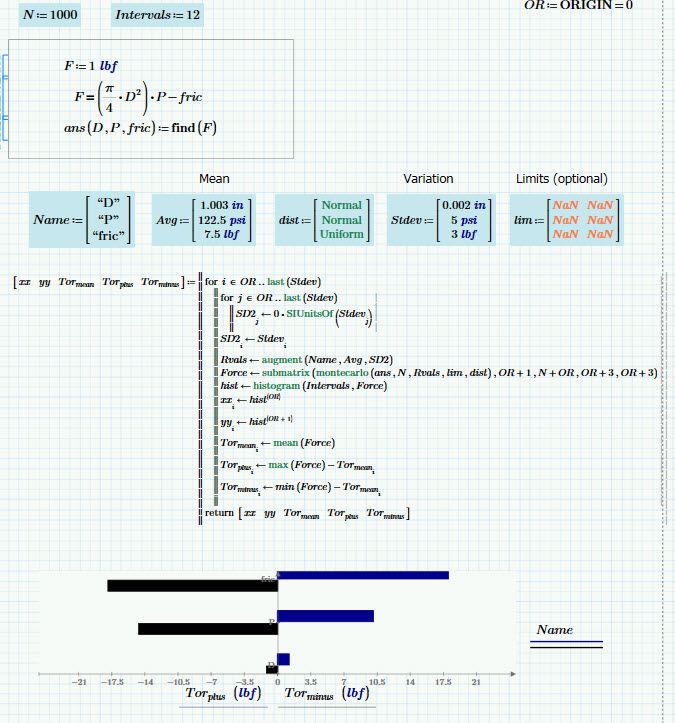
I came up with this to make a tornado graph (and histograms) from a monte carlo. The monte carlo is run several times, wherein only one variable is allowed any deviation at a time. Not the prettiest graph, but gets the job done. (Simple calculation looking at force output of a piston where the variables are diameter, pressure and friction)
4.0 attached