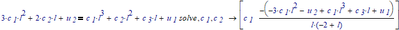Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
two eq. with two unknows.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
two eq. with two unknows.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Create a 2 element vector and put in the equations. It's simple.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well, first you must assume that c3 is constant. . .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think that Prime cannot solve a solve block symbolically.
But if you write it simply like this:
You get your answer, for c1 and c2 in terms of the other items in the equations.
Note that u3 is common to both equations, so your problem can also be described with:
This gives you a free choice for c1, then with u1, u2, c3 and l known, you can calculate c2.
Success
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
I think that Prime cannot solve a solve block symbolically.
That's correct. It would be possible to do so in real Mathcad (=Mathcad 15 and below) but they destroyed this possibility when they developed Prime. So the only way is to use the symbolic "solve" command as you had shown.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't understand, how do you put it like that, in a matrix or what?
Can you maybe send the mathcad file..
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Create a 2 element vector and put in the equations. It's simple.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There's more wrong with your sheet.
You define two equations with c1, c2, u1, u2 etc. these symbols are all labelled as constants.
Then you write the Find function where you want to solve c1 and c2, but these are labeled as <nothing>.
NOTE that a constant c1 is very different from a variable c1, or a unit c1 (if that would be defined).
Written like this, Prime can never solve it.
Success!
Luc