Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
why strange solutions obtained?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
why strange solutions obtained?
a simple example, but got strange results. while matlab can give reasonable answers, but i dont like the matlab codes. see in attached
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe it would help if you explain why you think that the result is wrong and what result (Matlab screenshot) you expect.
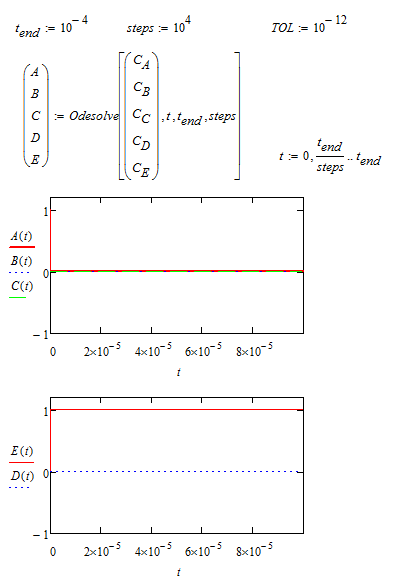
You want the system to be solved for a time interval up to 10^4 but you allow just (the default) 10^3 steps. A step width of 10 time units maybe is too large for a meaningful result. You may consider to solve for a smaller time interval and/or increase the number of iteration steps (thats an additional argument of odesolve).
I tried and the result is that A(t) goes down to zero right at the beginning when the precison is enhanced that way.
It looks like A is transferred amost immediatly to E, which is, looking at your coefficients k, no big surprise. Could it be a problem with numerical precision or what result did you expect? Your coefficients are rather big and k3 and k5 seem to be nearly neglectable compared to the others. Are you sure you used the same equations and the same coefficients in Matlab?
Can it be that it should be
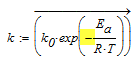
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe it would help if you explain why you think that the result is wrong and what result (Matlab screenshot) you expect.
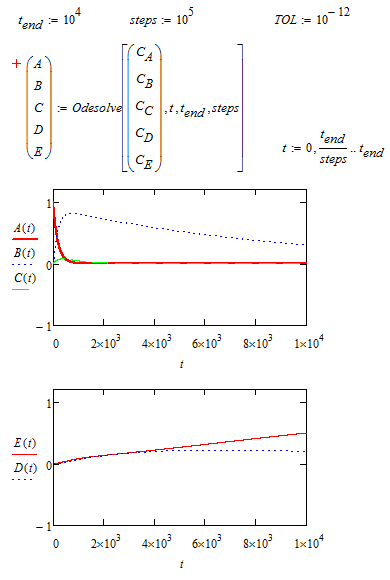
You want the system to be solved for a time interval up to 10^4 but you allow just (the default) 10^3 steps. A step width of 10 time units maybe is too large for a meaningful result. You may consider to solve for a smaller time interval and/or increase the number of iteration steps (thats an additional argument of odesolve).
I tried and the result is that A(t) goes down to zero right at the beginning when the precison is enhanced that way.
It looks like A is transferred amost immediatly to E, which is, looking at your coefficients k, no big surprise. Could it be a problem with numerical precision or what result did you expect? Your coefficients are rather big and k3 and k5 seem to be nearly neglectable compared to the others. Are you sure you used the same equations and the same coefficients in Matlab?

Can it be that it should be
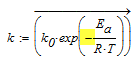

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank u very much for the explainations!
The keyponit lies in the negative symbol before activie energy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fan CG wrote:
Thank u very much for the explainations!
The keyponit lies in the negative symbol before activie energy.
Yes, Werner is one "minus guru" ![]()
See please http://communities.ptc.com/message/260444


