Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
x,y,& z parametric equations and 3-d plot
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
x,y,& z parametric equations and 3-d plot
Greetings,
I am trying to build a mobius strip in Prime 2.0
I have, what I believe, the equations in x, y, & z defined (found at Wolfram Mathworld), along with the other variable required.
The trouble is plotting the equations.
Attached is the file with what I have so far.
Any clues as to how to build the surface would be appreciated.
TIA,
P. Quint
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime's 3D-plot capabilities are very limited.
You may try an approach using "CreateMesh":
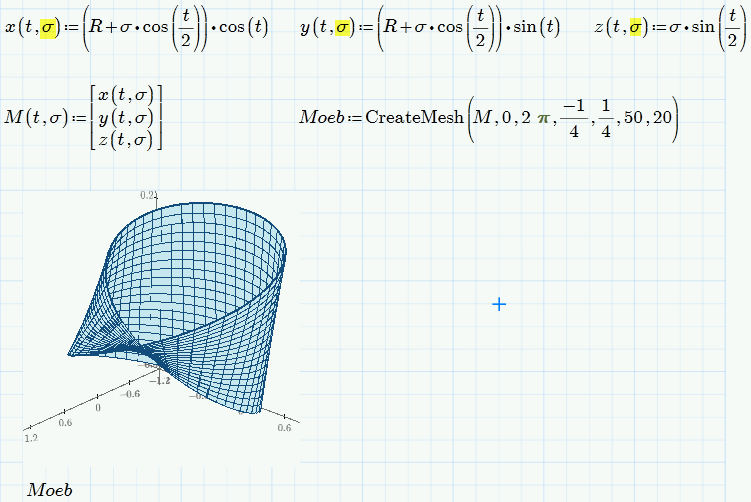
You might be interested in these links, too:
http://mpasternak.wel.wat.edu.pl/RekreacjeM/mobius.pdf
Click the picture below to see the animation (made with Mathcad 15):
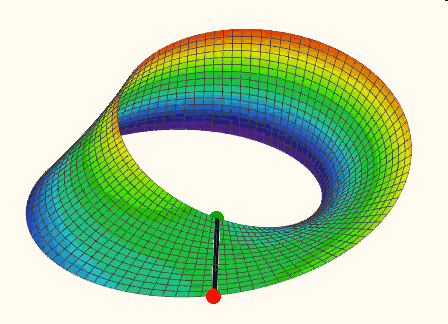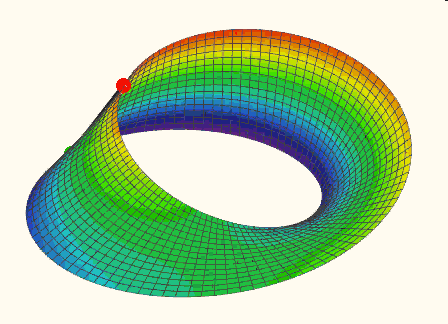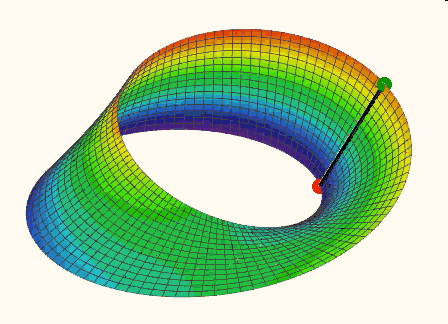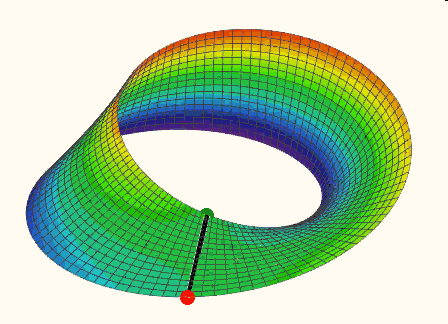
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime's 3D-plot capabilities are very limited.
You may try an approach using "CreateMesh":

You might be interested in these links, too:
http://mpasternak.wel.wat.edu.pl/RekreacjeM/mobius.pdf
Click the picture below to see the animation (made with Mathcad 15):

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Mr. Exinger!
From http://mpasternak.wel.wat.edu.pl/RekreacjeM/mobius.pdf and your pic, I can see why; the x,y, & z equations contain two variables.
But, in the formar, the relationship between w & v is not defined.
I'm going to assume that the sigma is the same as defind in my worksheet.
I'll give it a go and let you know,
PLQ
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Peter Quint wrote:
Thanks Mr. Exinger!
From http://mpasternak.wel.wat.edu.pl/RekreacjeM/mobius.pdf and your pic, I can see why; the x,y, & z equations contain two variables.
But, in the formar, the relationship between w & v is not defined.
I'm going to assume that the sigma is the same as defind in my worksheet.
In that sheet w seems not to be used at all.
The function argument you called sigma is called v in that sheet.
Imagine a vertical line segment which is rotated about the z-axis. The surfaced covered is part of a clinder. Now we additionally rotate that line segment around its midpoint (in a plane which includes the z-axis) so, that when the midpoint has described a full 360° circle, the segment has turned by 180° (half speed, thats where the t/2 is coming from. Now we get the Möbius surface. The midpoint has to travel two times around for all to be in the initial position (see the animation in my last post and watch the red and green end points of the moving line segment).
The variable a in the linked sheet controls that second rotation of the segment. If you chose lower values than 2, you get more twists of the band.
BTW, if you wonder why the plot in Prime doesn't look like the animation and other pics you usually find. Thats because of the scaling. In Mathad 15 I had chosen "equal scale". This is one of the many fearures not available in Prime. So you will have to scale all three axis individually to the same scale to get a similar effect.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now I understand creatmesh (& createspace). Though for sigma min & max, I set it to +-w.
This is cool.
PLQ
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Peter Quint wrote:
Now I understand creatmesh (& createspace). Though for sigma min & max, I set it to +-w.
This is cool.
PLQ
You don't need to use CreateMesh in Mathcad (15 and below), but without it you will have to set the limits for the two function arguments in the plot format menu (tab: "quickplot"), which I think is more cumbersome than using CreateMesh, where you can change parameters more quickly and are able to use variables.


