Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Happy Pi Day
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Happy Pi Day
For all the mathematics fans out there, I wish you a Happy Pi Day (3/14); celebrating everyone's favorite mathematical constant
Here are some ways to celebrate >>
-Dan
- Labels:
-
Other
- Tags:
- mathematics
- pi
- pi_day
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dan,
I have some problems with your statement, on mathematical and logic grounds.
- 3/14=0.2142857.... which is far away from 3.14159265....
- While it is easy to prove that there exist no uninteresting numbers, I doubt that you can prove that Pi is everyone's favourite mathematical constant.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To me, e seems more natural ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
To me, e seems more natural
Agreed. I'm a great exponent of eating πie off a log table made from the branches of trees with square roots (although some think this is rather radical, I think it's an integral part of the experience; it's what differentiates the true mathematician from the remainder)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, under the right circumstances a good πie can be an almost transcendental experience; the complex flavors can transport you to an imaginary domain. Nevertheless, whether or not π is 1’s favorite mathematical constant is a function of 1’s personal preferences. Clearly, in sum ways π is greater than e, but e has it’s base of supporters too.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Stuart, Richard,
Pi must be baked at the correct Degree or it will not achieve a Golden [brown] Ratio. I'm Maxed out on my mathematical play on words because I'm a Square.
Binomial for now,
Dan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
I must ask, do you have a personal favorite if it is not Pi?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dan,
I always felt myself more intrigued by e.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Students in Russia know the second math constant e as 2.7 (all know it) + two times... Leo Tolstoy - a year of him born - 2.718281828.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Happy pie day ![]()

Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike Armstrong wrote:
Happy pie day
Yes - three base math constants - p (p+Ctrl+G), i and e.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike,
Where's the vanilla ice cream?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here you go - there goes the diet.....

Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
there goes the diet.....
I though a slice of pie, rather then the entire pie, with only two scoops of ice cream was the diet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I though a slice of pie, rather then the entire pie, with only two scoops of ice cream was the diet.
Oh yer, good point. (As he heads back to the frezzer for the rest of the tub) ![]()
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
DanMarotta wrote:
Mike,
Where's the vanilla ice cream?
Look, enough of the food, already. Where's the beer? Being pi-eyed is the ultimate tribute to our e-ponymous number!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I do have one issue:- I can't believe anyone celebrates pie day like pancake day.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
VladimirN. wrote:
Happy pi/pie day:
More practical Pi-pie

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
More about Pi day and Pi Pie (Fractions).
Why I did not have Mathcad with gcd function in the first class of my school ![]()
See more about this problem here - http://communities.ptc.com/docs/DOC-3522

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Happy Pi, e & i day.
The 6 of the Mathcad Clock has Pi, e & i - 3 base Math constants:
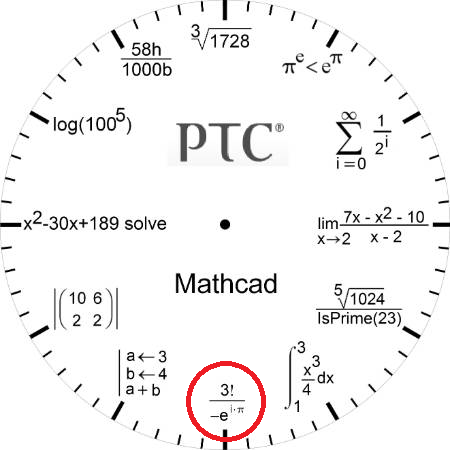
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

I'd like to remember Pi Day by making reference to one of your previous posts, Valery. (I could not think of a good reply to your remarks about Laplace transforms, so I did not post there.)
A circular slide rule is compact precisely because it wraps a linear slide rule around the circumference of a circle. The key to the transformation is pi.
Here is a snapshot of my own circular slide rule, a Sama and Etani "Model 90" (the diameter is 90 mm). Note that the "1" indicator on the C scale is lined up with pi on the D scale. So slide (rotate) the red indicator around to 9 on the C scale (for 90 mm) and read off 2.83 (i.e., 283 mm) from the D scale. Therefore, pi times the diameter 90mm is the circumference 283 mm.
Since there are 25.4 mm to an inch, we get 283/25.4 = 11.1 inches. To do this division on the circular rule, rotate the C scale until 2.54 is beneath 2.83 on the D scale. Then the C scale's "1" indicator points to 1.11 (11.1 inches) on the D scale. So our circular slide rule is equivalent to an 11-inch straight rule, at least for multiplication and division, since they use scales near the circumference of the rule.
Pi rules!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
RogerMansfield wrote:
(I could not think of a good reply to your remarks about Laplace transforms, so I did not post there.)
I was very sad when it has not received replies to a comment about the Laplace on the forum on Slide rule.
Variants:
- I'm wrong
- My colleagues on the forum do not understand this fine topic
- ???
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I do think that you are right, and for my part, I did understand. But all I could think of to add to that discussion was that I thought your demonstration was very insightful. It occurred to me to attempt to prove your results using the definitions and properties of Laplace direct and inverse transforms, but I just don't have the time right now to go in that direction ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When I was a student it was high art get mantissa and evaluate the order (power?) of the numbers on the slide rule ...
I have have have have numbers!
But now... With computer...




