Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solving an integral equation (with MathCAD)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solving an integral equation (with MathCAD)
Hi everyone,
I would like to know if there is a way in MathCAD to solve such an equation:
Where (unfortunately ![]() ) Sa(w,x) is known and G(w) is unknown. All other parameters can be considered known.
) Sa(w,x) is known and G(w) is unknown. All other parameters can be considered known.
The equation comes from a book about Eartquake Engineeering, and gives a possible relationship between Response Spectrum and Power Spectrum, together with Fourier Spectrum (less common) they are the type of spectra commonly used in earthquake engineering.
So the unknown function G (in my problem the power spectrum) would appear at the same time under integral and outside of it. Schematically it would be something like:
with F(w) known (but not a simple analytical function, it would have to be a splined interpolation, see small example on the left in the first picture above) and X(w) unknown.
If, as I believe, there is no MathCAD way, I would be grateful for some hints to known numerical methods to solve the problem... my calculus lessons are a little dated ![]()
Thanks a lot in advance
Claudio
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Wouldn't it be possible to differentiate both sides of the equation and obtain a differential equation which Mathcad possibly could solve numerically?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Wouldn't it be possible to differentiate both sides of the equation and obtain a differential equation which Mathcad possibly could solve numerically?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Differentiate with respect to w0 to obtain a differential equation in G(w0):
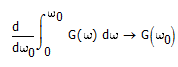
BTW, it's bad practice to use the same variable name for the variable of integration and the limits of the integral, because they are not the same variable ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well, thanks a lot to both of you, Werner and Richard. That was easy enough, I just didn't think of this. It should work, I will have to think a little about the initial conditions, but I will certainly give it a try.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The initial condition is the lower limit of the integral, so substiute this into your equation 5.9:
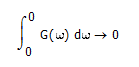
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It took a little time because I was busy on something else.
I just wish to inform both of my helpers 🙂 that thanks to your suggestions the equation 5.9 could be solved (I used an odesolve block), and the complete solution is in good agreement with the simplified solution provided by 5.10, for my special case. I do not post the complete solution because it is very specialized to my problem, but it worked perfectly.
Just out of curiosity, what's than the matter with integral equations? I was under the impression that they are much much difficult than "normal" differential equations. Possibly I am misunderstanding the real meaning of "integral equation".
Anyway thanks a lot. This forum is one where I always get immediate and competent answers, which is not always the case on the internet 🙂
Have a nice day
Best regards
Claudio
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Glad you found your solution. I guess the trickiest part was finding the initial condition.
Just out of curiosity, what's than the matter with integral equations? I was under the impression that they are much much difficult than "normal" differential equations. Possibly I am misunderstanding the real meaning of "integral equation".
Integral equations sure are much more difficult to deal with compared to differential equation. But there are very simple differential equations which can simply be solved by a single integration and so we also have easier integral equations which can be turned into a DE by differentiation.
The lucky part in your equation is that the variable (omega0) does not appear in the intgeral but as the upper integral limit.


