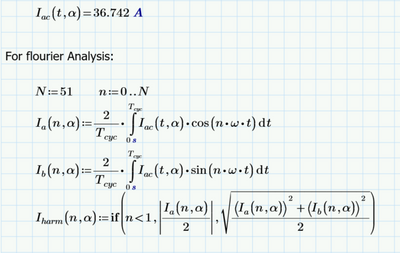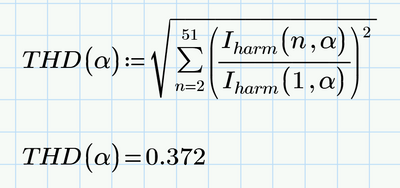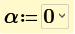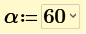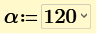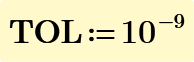- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Total Harmonic Distortion of AC current using Fourier Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Total Harmonic Distortion of AC current using Fourier Analysis
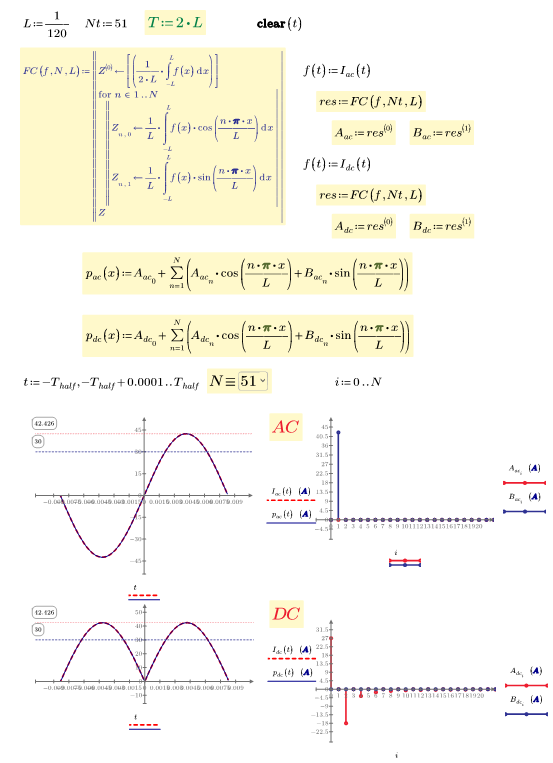
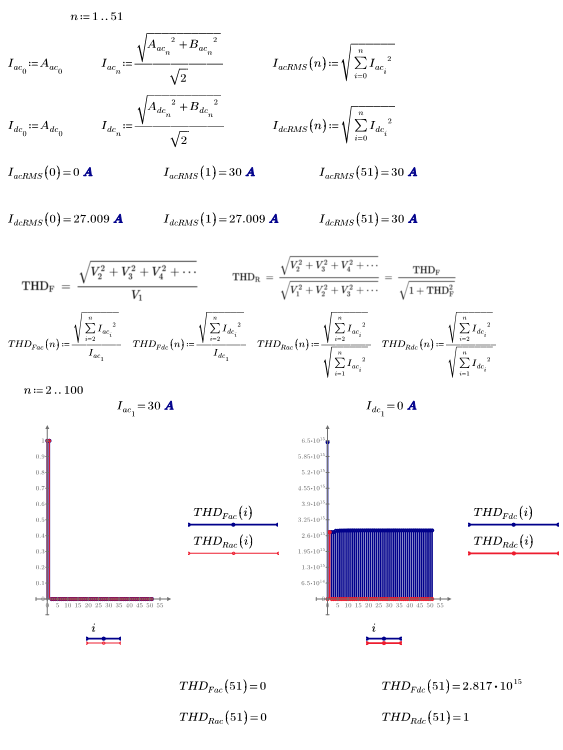
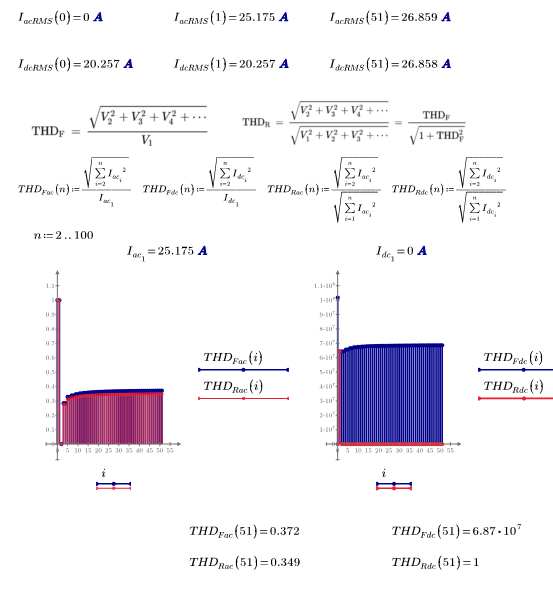
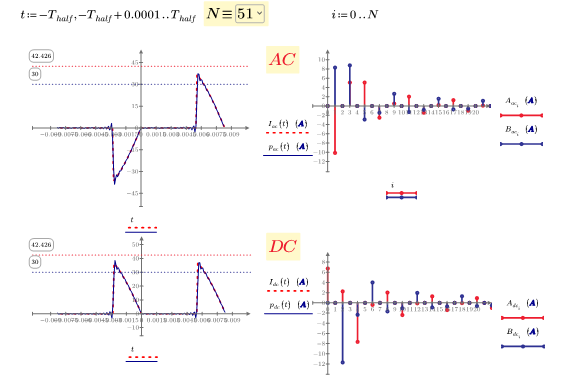
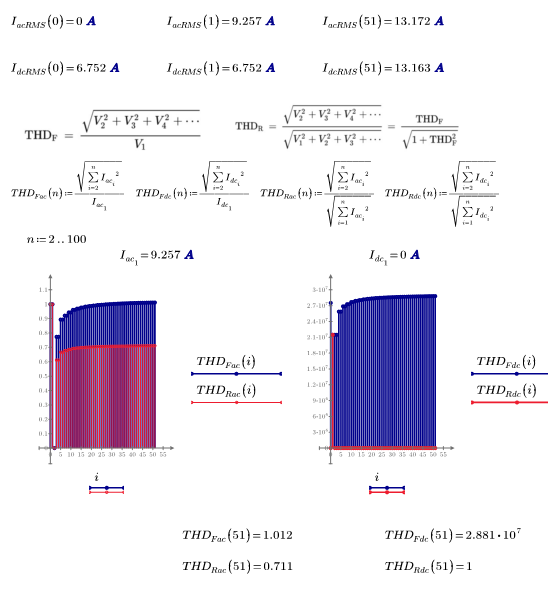
So, I've been able to work through all the values so far but seems like I have a problem with the summation notation since the THD of alpha does not converge to a solution:
Solved! Go to Solution.
- Labels:
-
Electrical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not sure why, but the problem is "only" n=2 and function I.a
The function you integrate does not look malicious
Some additional observations:
EDIT:
Solution - Set the system variable TOL to a lower value. Either write TOL:=10^-8 at the top of the sheet in front of the function definitions or use the menu.
Doing so makes the integral converge
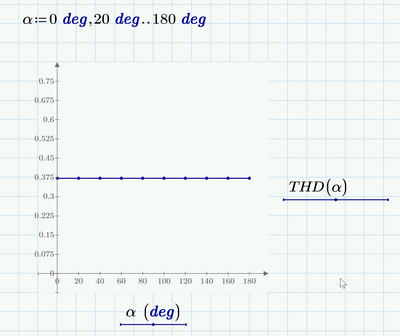
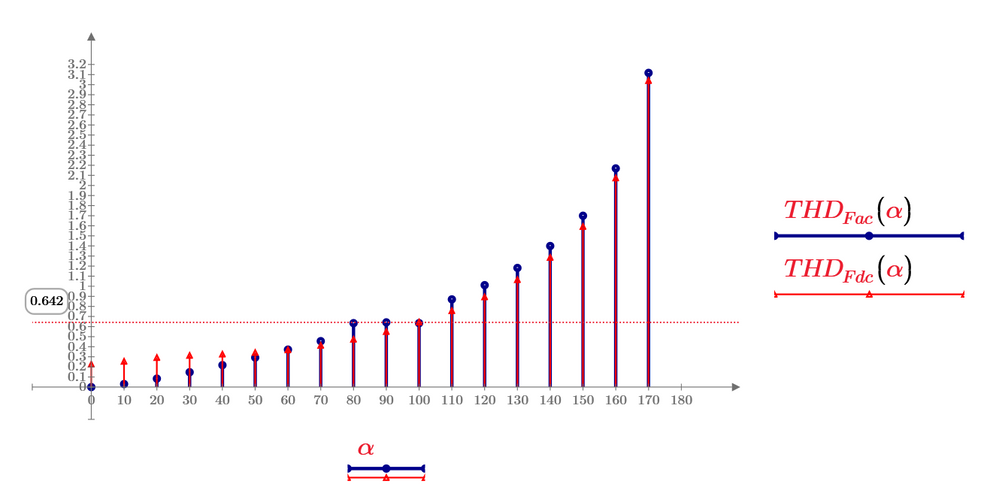
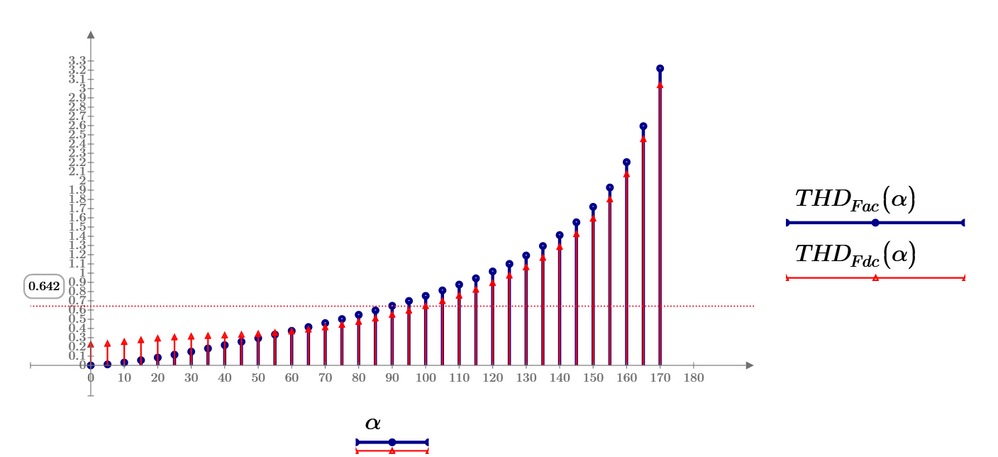
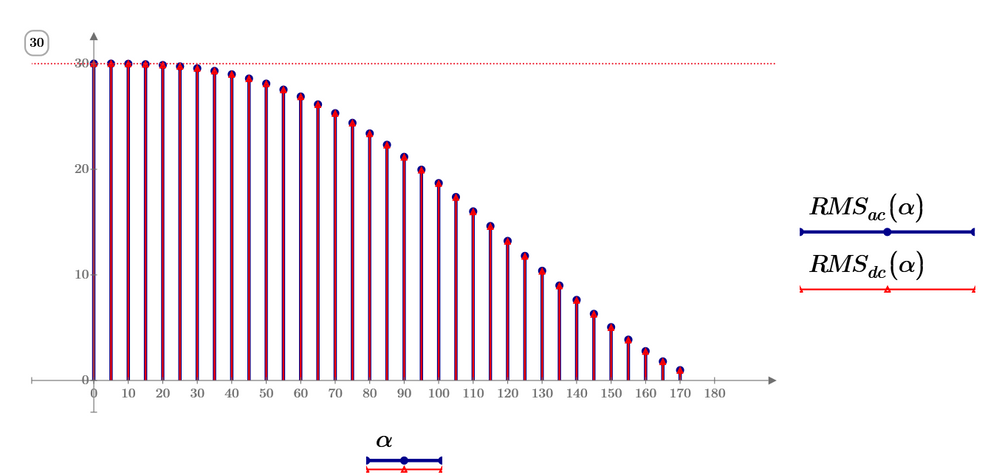
The plot below with variable values of alpha takes very long. I stopped it and used a larger step width to speed it up.
It looks like THD is independent from alpha
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
File?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I get a notification saying I can't post the file using the email, is there any way to attach the file here?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Drag and drop.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not sure why, but the problem is "only" n=2 and function I.a
The function you integrate does not look malicious
Some additional observations:
EDIT:
Solution - Set the system variable TOL to a lower value. Either write TOL:=10^-8 at the top of the sheet in front of the function definitions or use the menu.
Doing so makes the integral converge
The plot below with variable values of alpha takes very long. I stopped it and used a larger step width to speed it up.
It looks like THD is independent from alpha
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Great Werner_E! Well done! Congratulation
walter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its not that difficult to track down errors like this using "try..on error".
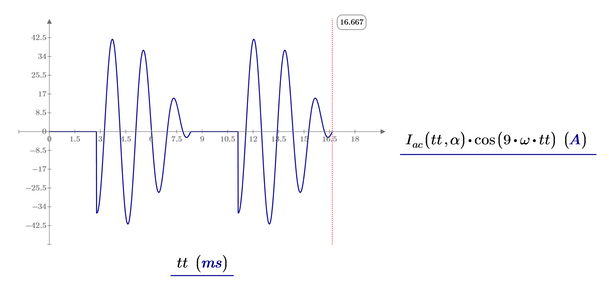
It was surprising that just the single value n=9 threw the error and all others worked fine.
The usual way would be to increase the value of CTOL and see if convergence could be achieved that way. Not sure why I had the idea to decrease TOL 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for the tip. Its interesting to find out why value of n=9 creates an error. I appreciate your help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@cadtelsim wrote:
Thank you for the tip. Its interesting to find out why value of n=9 creates an error. I appreciate your help.
Yeah, if you find out, let us know.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for the detailed analysis. This complete analysis will be instrumental in learning features of Mathcad along with the limitations of THD of ac current related to the delay angle. I'll fully study this document.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To calculate correctry, TOL is sensitive and integral from -L to L gives bug error at 80 to 100 degree.
Divide it from -L to 0 and from 0 to L makes good answer. Prime 9.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for the detailed response. I will do my best to replicate this to understand Mathcad features better.