Here's a little problem that customers run into every once in a while and a way to get around one of Creo Simulate's limitations.
Suppose you have a laminated composite with a quasi-isotropic layup (say, [0/+-45/90/90/-+45/0]) and you know only its equivalent smeared properties, which are equivalent to a transversely isotropic material. Or perhaps you have some other material that is transversely isotropic. Now suppose you want to assign that material to a shell idealization with the unique direction normal to the shell. How do you do that? Unfortunately, it's not as easy as it should be.
When specifying a transversely isotropic material on the material definition dialog, the unique direction is the 1 direction and the plane of isotropy is the 2-3 plane.
Figure 1
To specify how this material is aligned in your model, you need to define a Material Orientation. The 1, 2, and 3 directions of the material orientation correspond to the 1, 2, and 3 directions of the material. However, for material orientations applied to surfaces, the material orientation 3 direction is always normal to the shell's surface, as shown below.
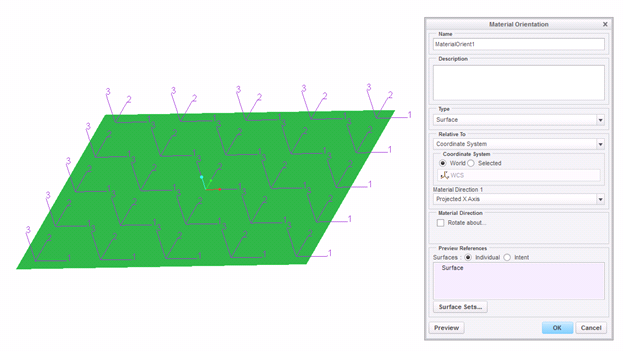
Figure 2
There's no direct way to make the materials 1 direction to be normal to the shells surface.
The work around is to define an orthotropic material that is equivalent to the transversely isotropic material.
Suppose the transversely isotropic material is as show above. The equivalent orthotropic material is
Figure 3
G23 was calculated using the formula,
G23 = E2 / (2 * (1 + nu32))
as shown in figure 1.
But the unique direction of this material is still the 1-direction and the plane of isotropy is the 2-3 plane. We want to define a material for our shell with the Young's modulus in the normal direction of the shell equal to 10 GPa. Therefore, we need to define a material with E3 = 10 GPa, and with E1 = E2 = 200 GPa.
In other words, we want to swap the 1 and 3 directions for our material. Calling the old directions 1/2/3 and the new directions 1'/2'/3', we want to perform the swap:
1 -> 3' 3 -> 1' 2 -> 2'
E1' = E3 = 200
E2' = E2 = 200
E3' = E1 = 10
G1'2' = G32 = G23 = 76.9
G1'3' = G31 = G13 = 50
G2'3' = G21 = G12 = 50
nu2'1' = nu23 = nu32 * E3 / E2 = 0.3
nu3'1' = nu13 = nu31 * E3 / E1 = 0.6
nu3'2' = nu12 = nu21 * E2 / E1 = 0.6
where I used the relations:
G_ij = G_ji
and
nu_ij = nu_ji * Ej / Ei
(Creo Simulate use's Tsai definition of Poisson's ratio.)
So the material definition dialog is
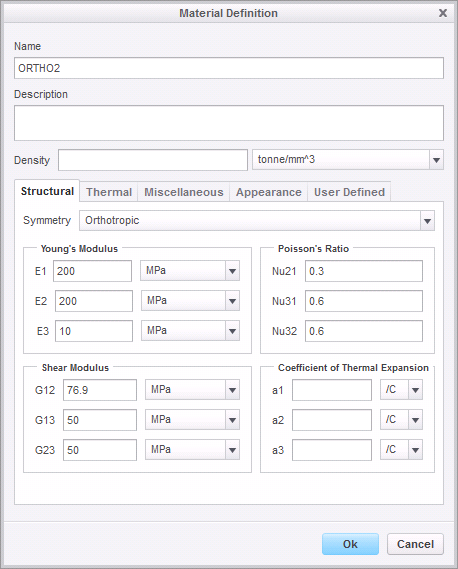
Figure 4
