Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Community
- Creo+ and Creo Parametric
- 3D Part & Assembly Design
- Need help regarding 3 point constraint system
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Need help regarding 3 point constraint system
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Need help regarding 3 point constraint system
I created a simple analysis with a 3-point constraint system for a plate with hole in it (the part is attached in zip file with this post)
However whenever I try to analyse the part, it keeps throwing the following error:
The unconstrained degree of freedom can be seen by running
a constrained Modal Analysis with rigid mode search.
Animating the rigid modes will display the unconstrained
degrees of freedom. If the error still occurs, then the
issue could be caused by material properties or unattached
spring/mass idealizations.
How do I fix this problem?
This thread is inactive and closed by the PTC Community Management Team. If you would like to provide a reply and re-open this thread, please notify the moderator and reference the thread. You may also use "Start a topic" button to ask a new question. Please be sure to include what version of the PTC product you are using so another community member knowledgeable about your version may be able to assist.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
i have had a quick look at your part and i can see it is modelled as a plate with a quarter hole. You should therefore use symmetry constraint on both symmetry surfaces. But only if the load in the model is also acting symmetric. If the load is not acting symmetric you will have to model the full part. I have run the model with symmetry constraints and is solves just nicely. You might have to increase the element density thou!
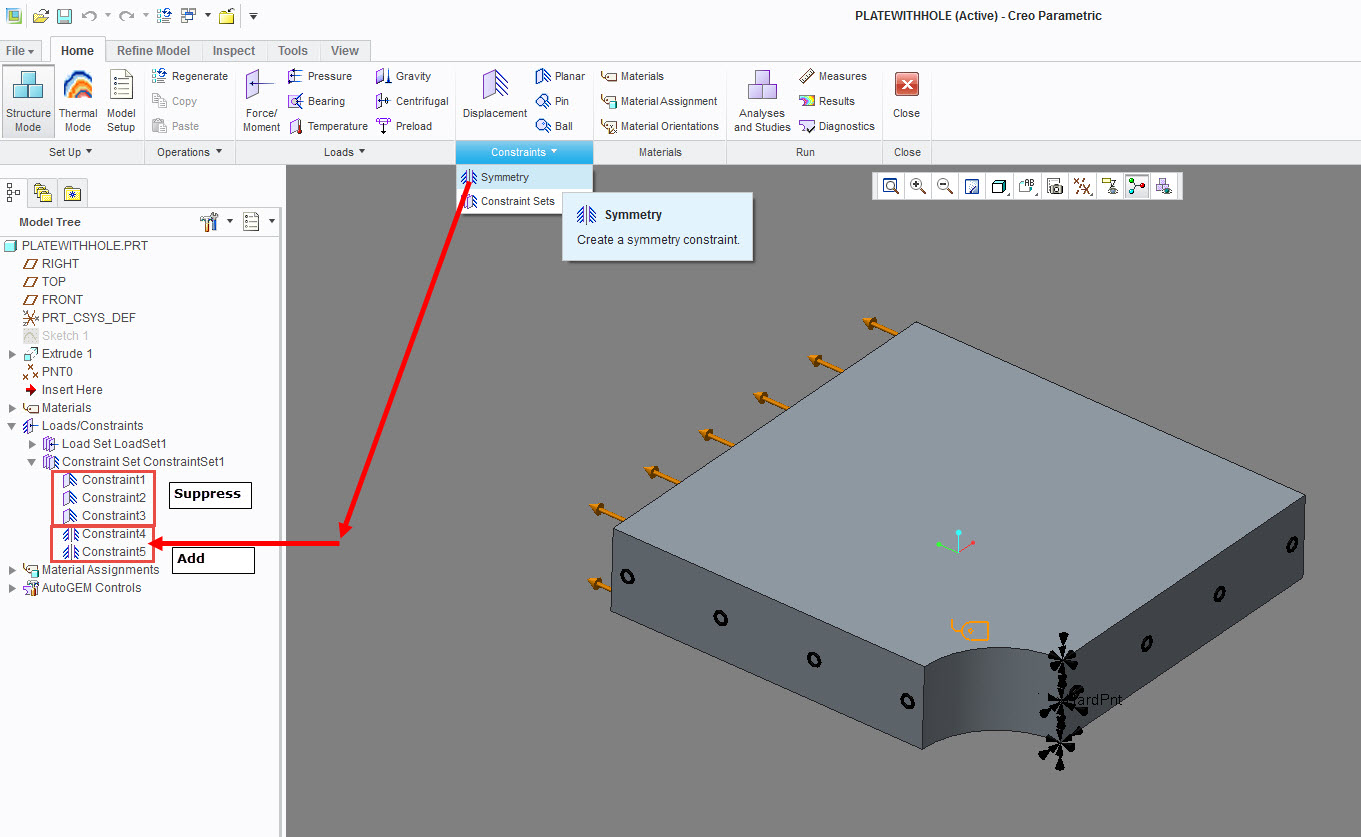
Best Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the more general case, the text in the error is actually really helpful for once.
"[R]un...a constrained Modal Analysis with rigid mode search. Animating the rigid modes will display the unconstrained
degrees of freedom."
The animation should clearly show you how your model is unconstrained. You only need the first mode or two, and a Quick Check should be sufficient, so it should run reasonably fast.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Lucky,
You have 3 points with constraints, one with 3 translations fixed, one with 2 translations fixed, and one with 1 translation fixed. So far so good.
A few things are going wrong though:
* You are constraining rotational degrees of freedom, but this will have no effect, because you solid elements in you part. Solid element nodes have only 3 degrees of freedom: the 3 translations. Normally what you did will not cause any issues (except a frowning face on some FEA people), but in this case it is not so innocent. (This is probably a good example why you should not tick those rotational constraints when using solid elements)
* Your three points are on one line. Due to that, you still leave one degree of freedom open: rotation about that line. Maybe you thought you had that covered by constraining the rotation of the nodes, but that is not the case. The rotational constraints are ignored, without warning. (PTC should really issue a warning, considering their FEA software is supposed to be for people with little knowledge about these things!)
So the fix: move your 3rd point to be away from the line through the first 2 points, and carefully rethink your constraints, so that you do not have any "overlapping" constraints.
Think of having a free body. On one point you put a constraint on 3 translational directions. The body is now fixed in space, but can still rotate in three directions around that point. Now you pick another point and constrain the 2 translations which are perpendicular to the line between the points. You have now constrained 2 rotations of the body, but it can still rotate around the line between the points. So the final point should be away from that line, and the constraint should be perpendicular to the plane through all 3 points. Now you have fully constrained the body, for all translations and all rotations, but the body is still free to deform in all directions. This is a very minimalistic way of constraining the body.
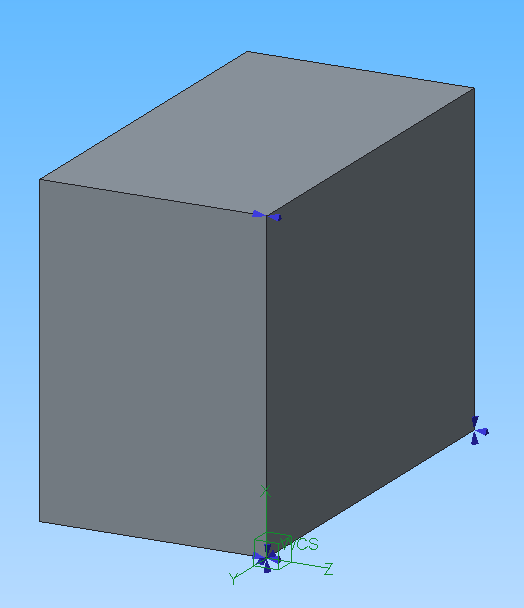
If you require symmetry, which seems to be the case here, the above method it is not enough, because you need symmetry constraints. These symmetry constraints will make some (or all) of the 3 point-constraints superfluous.
If you were to model the plate with hole using shell elements, the story also changes, because shell elements have nodes with 6 degrees of freedom.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Jacob, Jonathan and Patrick.
I will incorporate all your suggestions into the analysis and check if I get the desired results for the quarterplate design.
I will post a reply as soon as I finish.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
The rule for applying the three-point constraint is as follows:
- The points can be anywhere on the model surface, but are not allowed to be collinear.
- Fix the first point in all translational directions.
- Fix the second point in the two orthogonal directions relative to the axis through point 1 and point 2.
- Fix the third point normal to the surfaces through all points.
The main problem with this, is that it leads to singularities if your model is not in equilibrium. In other words, you have to apply other loads in order to have a resultant of 0 for forces and moments on the entire part.
The image shows you how to calculate an opposite "equal" force of 250 Mpa that you have to add to your model.
The video shows you how to review the total load in order to find the equilibrium, notice the approximate values to 0.
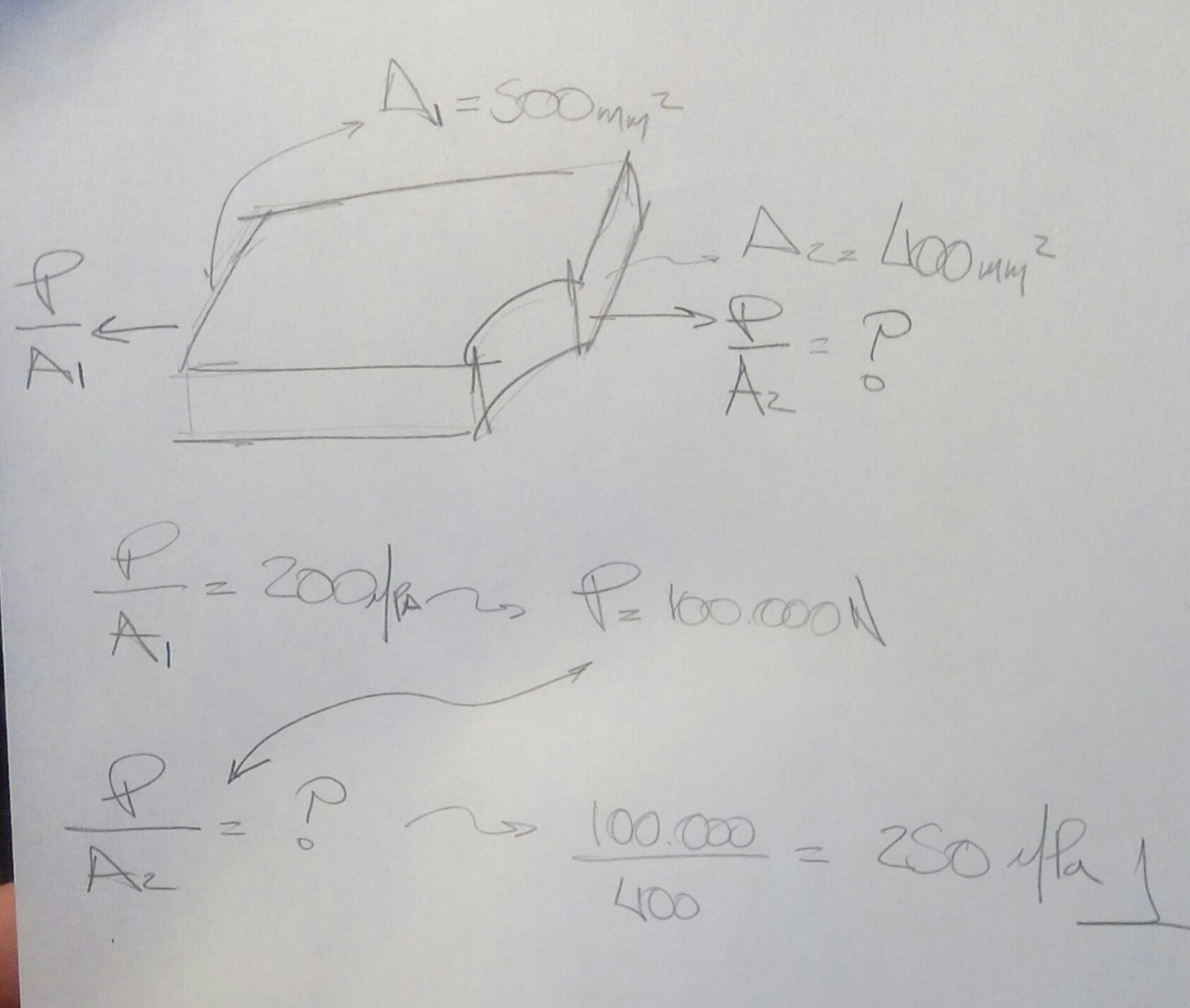
Note that this model does not have symmetry definitions, this is the final part and not a slice of it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
looking at your animation brings up a question. Your symmetry surface in YZ-plane seems to be moving "out of plane". This would not be the case if symmetry truly exists, right? In your simulation that would mean the mirrored part should also move "out of plane" into the modelled part, which sound a bit odd to. In my opinion the symmetry surface in YZ-plane should move only along the Y-direction, otherwise symmetry is not existing.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good point. That is because the moment is applied around a point. Depending on the choice of the point location, the deformations will look different.
If you model symmetry with help of constraints, these constraints may introduce reaction loads in your model. If you were to apply these exact same reaction loads in the model, you could then leave out the constraints, and you would end up with a similar model as in the movie. Adding up the reaction loads would also give a reaction moment equal in magnitude to the moment in the movie, but built up out of different loads. If one were to plot the reaction loads at the constraint locations, it would probably not look as neat as a total load at point.
But (I think) the idea here was not to show how to model symmetry with only loads, but rather how to put loads on a model without the need for constraints.
(Please note that only applying a 3-point constraint would also give non-symmetric results!)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The animation will look slightly different if you change the point location, because you are changing the resultant (that is approximate it to 0, but not 0). This of course will affect displacements and stresses, however the result is almost the same.
The image shows what happens with the resultant when you change the point location.
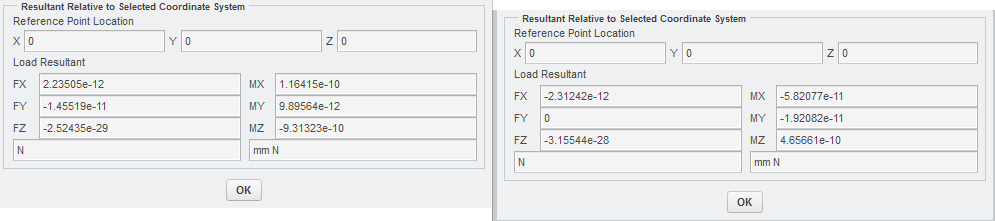
Jakob Warncke, you were right "In my opinion the symmetry surface in YZ-plane should move only along the Y-direction, otherwise symmetry is not existing."
In this model symmetry is not assumed, as I said before, this is the final part. Is not a slice of it, or a representation of a portion of it. The simulation has no symmetry at all. That's why you see the part moving in that way. With symmetry, that shouldn't happen.
The intention here is shown that if you apply the 3 point constraint, your model must be in equilibrium.
I guess that inertia relief is a better choice anyway.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting.
Another point that I somehow didn't yet see is that there will of course be a stress concentration around the hole, so the evenly distributed pressure on A2 is an incorrect approximation of the reaction loads on that end...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
after reading the whole thread again, i realized that i was the one bringing up symmetry constraints to begin with :-). This was not brought up by OP, i just assumed this based on the model provided. But this led to a good discussion and work around. Thanks
Regards





