Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Community
- Creo+ and Creo Parametric
- Analysis
- Torque Motor vs Servo Motor
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Torque Motor vs Servo Motor
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Torque Motor vs Servo Motor
Hello Everyone,
In a mechanism (no resistive forces other loads), if I provide a servo motor to a rotating link, it behaves as expected where very minimal forces are generated in links and I believe servo motor just gives enough power/velocity to cause motion. So If i put a measure for reaction forces at various links, the force values are very less.
However, If i replace the servo with a finite value torque motor, reaction forces (equivalent in the order of a static case) are generated in the links even when there are no other resistive forces.
I would be much obliged if anyone could explain the above.
Thanks in advance
- Labels:
-
Mechanism Design
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
please ask the same question to PTC Support, too.
Martin Hanák
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
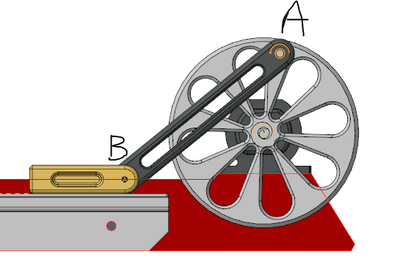
Here is a sample mechanism. In a friction less model, the measures of connection reactions at A & B are different when we use a torque motor at center of wheel vs servo motor (angular velocity input). Rx A and Rx B for servo are negligible values as the servo does bare minimum to move the links. But the reactions when run with torque motor are much higher and cannot be ignored. So what is causing this resistance and generation of forces at connections?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A servo motor will provide a constant angular speed (deg/sec) with a varying load. In your example, the flywheel will turn at a constant angular velocity.
A torque motor will provide a constant torque (kg m). In your example, the fly wheel will accelerate and decelerate based on the kinetic load of the system.
There is always more to learn in Creo.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello @kdirth
Thanks for taking a look. I totally agree with your explanation.
However, my original query was related to the "based on the kinetic load" part your response.
when there was no other load on the system (not even friction and no gravity), how come the torque motor still generates reaction forces at links?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Newton' 1st and 2nd laws of motion.
As the fly wheel turns, link pushes and pulls on the slider. The slider will oscillate, accelerating and decelerating. The mass of the link is also accelerating and decelerating as the flywheel turns.
With a servo motor, the speed of the flywheel is constant. With the torque motor, the torque of the motor is constant. The speed of the system with a torque motor is determined by when the when energy needed to accelerate the components equals the energy provided by the motor. I would guess that your servo motor may provide a speed of 100 rpm while the torque motor system balances out at 2500 rpm. making the forces much higher with a torque motor.
There is always more to learn in Creo.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi @kdirth ,
Thanks a ton for actively posting responses. I apologize for the late revert. I agree with your explanation in general. However, please take a look at the below scenario:
1. I have changed the densities to negligible values for all links under consideration so that we are dealing with the nearly massless system (and hence negligible inertial forces/reactions).
2. The flywheel has been trimmed down. This now resembles an 'eccentric slider crank mechanism'.
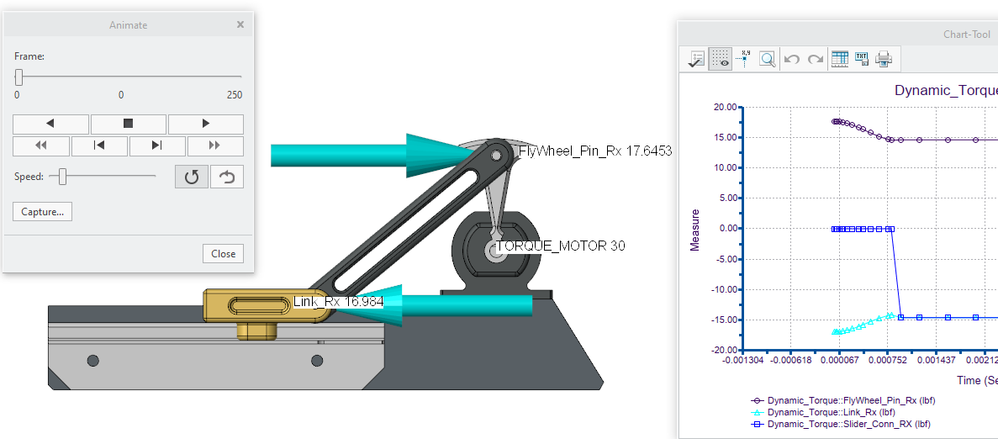
I have run a dynamic analysis only for a small rotation of the crank (trimmed down flywheel) for about 20degree angle. The way I'm stopping achieving this small rotation is by imposing a 'translation limit' on the yellow slider link. As usual, no frictions and gravity considered.
A torque of 30 lbf-in when applied at the crank center, the only resistances in the system should be the negligible masses in the black and yellow links, ... Until the translation hard stop is reached, the connection reaction at slider conn'n is zero as expected. Once hardstop is reached, the entire system reaches static equilibrium and the slider connection also shows the connection reaction. I have posted snapshots of (a)first frame (b) frame at static equilibrium. For sanity check I did the Free Body Diagram static equilibrium calc at the hardstop condition and I'm exactly able to calculate the X-Reaction. Now my query is:
a) The static equilibrium value calculated at hardstop exactly matches with creo and there is indeed a physical resistant to the slider (and hence slider connection reaction shows up).
How are the transient values calculated? (slider connection is zero).
b) I could get the transient Rx values by locking the mechanism at that rotation instants (before hardstop is reached) and can work out the FBD calculations. In this case, the reaction forces are all a function of the crank angle and it can be proved that the reaction forces are higher when crank is at 12'O clock compared to when crank is at say 10'O clock. Does creo consider static equilibrium at every frame rate as it generates the results?
c) It is indeed counter-intuitive to accept that the reaction forces are higher before the mechanism encounters the physical hardstop!
I'm extremely sorry for the long post, but this is how best I could communicate. If there is any way we could correspond directly, that would be great!
Appreciate your time again!