Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Community
- Creo+ and Creo Parametric
- Analysis
- modelling of tapered roller bearing for simulation...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
modelling of tapered roller bearing for simulation of system
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
modelling of tapered roller bearing for simulation of system
Hello all,
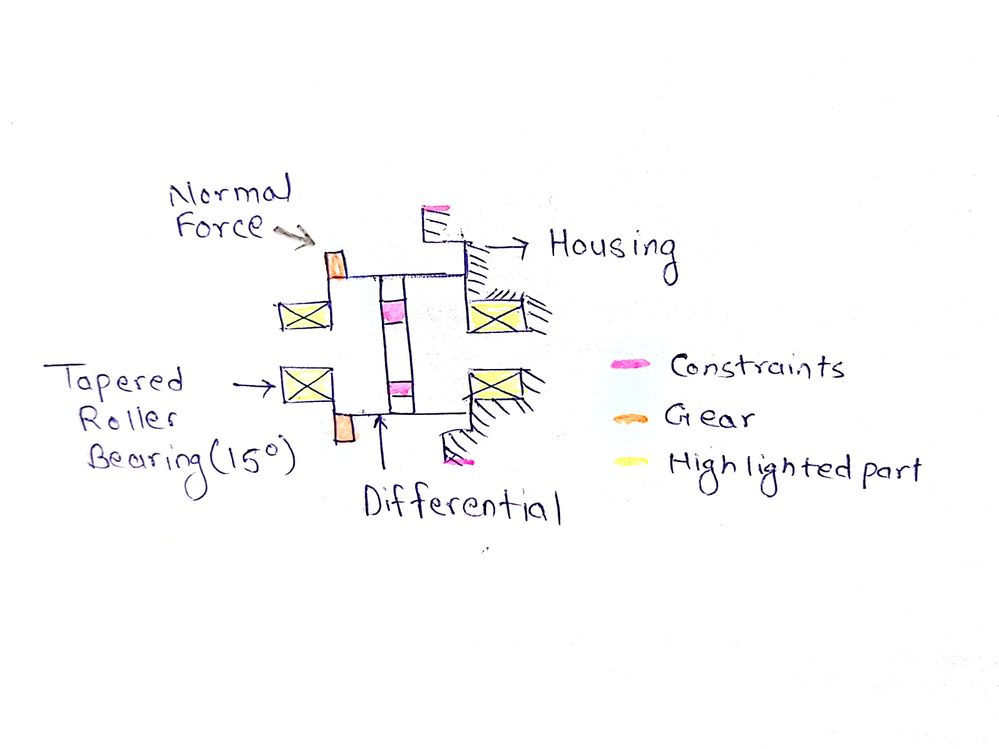
I want to construct a differential system which is supported by two tapered roller bearing on both the sides.
As we all know that in tapered roller bearing the forces are distributed in axial and radial direction depending upon the angle of the taper.
Is there any possibility of creating a parameter which would represent as tapered roller bearing in the system and transfer the forces further in the gearbox housing accordingly.
I am attaching a basic image which would give you the idea of forces and constraints but the transfer of force is through a bearing where the forces further applied on the housing linearly without any effect of taper roller bearing and this is creating some unwanted results which does not represent any comparable stresses and displacement done in the Real static torsion test on the model.
- Labels:
-
Simulate
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, I think the question is not clear. Also, getting correlation to a real test on this assembly might be beyond what the community can assist with. The details and time involved will be extensive and complex. There are many questions to pursue.
A more specific question might be "How to model a taper bearing constraint?"
Creo is challenged with a taper bearing constraint because it is not a nodal based method, whereas many other FEA programs are nodal based. My first approach might be to model not as a constraint but as a non-uniform load using an equation so the force vector is normal to the taper. (free body method with possible inertia relief) As a second approach, If I really needed to model the taper using displacement constraints instead of loads, I would do as follows.
Separate the bearing surface into many smaller surface regions with coordinate systems for each surface region pointing in the correct direction for constraining that local surface. This is essentially similar to how it would be done in a nodal based FEA system, where each node would have its own unique local coordinate system to define the direction for its displacement constraint. The main difference is in Creo, for a 3D model, surfaces need to be used because a point constraint makes a singularity.
Note that there needs to be a band of unconstrained surface between each region, otherwise it will be over-constrained at the shared edge. In my quick example the unconstrained bands are the same size as the constrained ones, but this should be adjusted.
In order to test that the bearing is free in rotation I performed a simulation with torque applied as this image shows.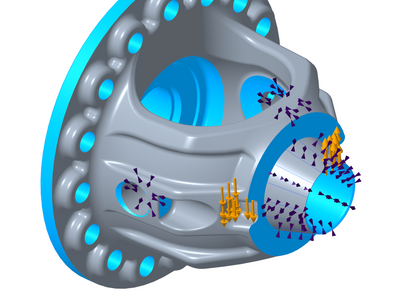
As you can see in the next image, the bearing surfaces can rotate with a torque applied, however they are distorted. This can be improved by dividing into more regions and reducing the size of the unconstrained areas between regions.
As yet another option, a complex but probably more accurate model would use contacts at the taper bearing instead of a constraint or load. The mating component(s) would be needed.
Finally, in the most simple case, I would think in many models the movement along the taper is negligible due to the taper bearing preload. So a simple constraint based on a cylindrical coordinate system would work (with R and Z , held, theta free.)
Maybe someone could ask the Creo developers if they can add "tapered pin" as a constraint type in addition to "planar" "pin" and "ball", or more generically "normal to surface constraint"???
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello SweetPeasHub,
Thank you for the reply. That's a good approach for having a taper roller bearing effect.
But i want to transfer the forces from the Differential housing to Gearbox Housing and in between i am having a taper roller bearing.
This taper roller bearing would modify the forces while transferring it due its nature. How could I create this effect in virtual analysis?
I am more interested in knowing the different possibilities of modeling the same rather as having direct results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not experienced in it, but the force transfer capabilities of the taper bearing should be able to be modeled.
I am ok with approximation so I would probably model the bearing as two wedges where the material of those wedges models the bearing stiffness and the angle between them models the force transfer from radial to axial and vice-versa. This would be a force equivalent angle, not necessarily the actual angle in the bearing, but probably close. The wedges would have a contact (maybe with some small mu) defined between them and either bonding or contact to the mating housings. Some proof by calculations and simple FEA studies of the approximation could compare and help tweak this equivalent model to a more detailed FEA of the bearing, or to standard taper bearing hand calculations and load factors.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hallo skunks,
Es geht schon für mich
Danke
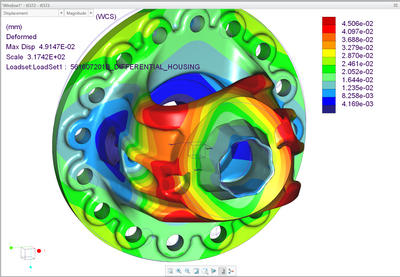
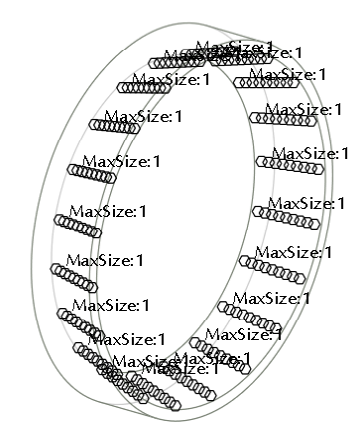
Can you put some light for these two images?
What should be the stiffness of the springs in the first image?
Also, i do not understand
what is defined in the second image?
the circles
what is its importnace?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1. for example: K=10N/mm for x, y, z
2.
on curves
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Danke Skunks!
Ich verstehe auch ein bisschen Deutsch
...and there is always google translate. ![]()
I was contemplating how to keep those bearings from flying around.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hey skunks,
I have tried the same as explained in the presentation.
But I am getting an error that The model is insufficiently constrained for the analysis.
What could be the possible cause?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
constraint
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How could we know the Convegence percentage or the model is totally converged or not?
Do we have to play with meshing all the time or is there any self-analysis to be done or any function in creo?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here the iterations are 49
And
Residual norm tolerance: 1.00000e-12
So this model is corverged 100%
??
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
49 iterations are nice
but what is:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I dn know actually
In other Calculation. It is 0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
load factor 0 => iterations 0
load factor 1 => iterations XX
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, but i didnt understood
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
do you have fastener?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
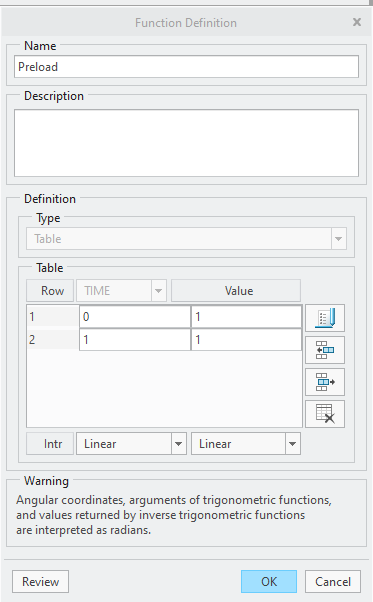
No but i have preload with fuction
And in the second step i have
it was a 8 step calculation and in the 8th step it is showing 1
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ok, very good.
why 8 steps?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I WANT TO SEE THE ANIMATION............ in the result
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
all is ok
🙂