Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Community
- Creo+ and Creo Parametric
- 3D Part & Assembly Design
- Re: create exit curve
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
create exit curve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
create exit curve
Hi all,
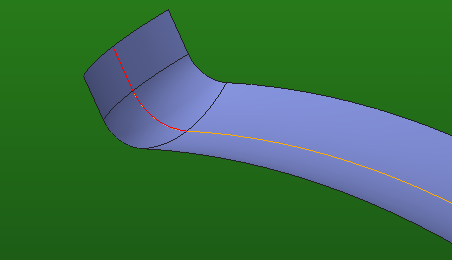
I require a help to create sweep using a helical curve and normal exit curve has shown in the figure .
I require support to create a exit curve which is tangent to the helical curve , so that I get very smooth sweep feature by combining these two curves
- Labels:
-
General
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Use spline curve in sketch
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
hi skvarka,
I also tried with spline but it didn't work , if feel the helical curve and exit curve should be tangent , but question is how can we draw tangent to helical curve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I dont know what you mean with exit and helical curve. There are tangent constrint in your image.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have two curve one is exit curve which is a straight line with radius and the second is helical curve basically we need to combine these 2 curve to create a sweep feature.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I take it, that the helical curve is a 2D curve, too? In this case it should be sufficient to use the constraints as shown in the image
(use the end of the curve). You can also use centerlines to make sure that the constraints are correct.
If the helical curve is a 3D curve, a 2d exit curve won't work, because you'd need 3d tangency.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the helical curve is 3D
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In that case, you'll have to create a 3D curve, there are many ways to create those.
For example, create points, and then create curves through points in 3d. Start with a point at the end of the helical curve and add a axis for a tangential reference.
Alternatively, extrude the exit curve to a surface and use this as project surface for a second sketched curve.
Or, take your exit curve and create a second one perpendicular to the first and tangent to the helical curve, then use Intersect.
It's hard to tell without knowing the runout geometry of the helical curve.


