Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Rank matrix with mixed units
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Rank matrix with mixed units
Is it an error in Prime or I do somethink wrong? The Prime 2 sheet in attch.

Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solution:
But I think not all is correct in Prime! Jakov Kucan, where are yuo!?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think it is an error. Or?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't think it's an error. To find the rank of a matrix one has to perform some operations that involve subtraction of terms from different rows. This only makes sense if all the terms in the matrix are of the same type. The determinant works for your examp;les because items of different type are only multiplied together (which can make sense).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fully agreed. I, too, won't consider this an error.
This only makes sense if all the terms in the matrix are of the same type.
And thats the reason the numeric processor fails - its aware of units. While I don't consider it a bug or error I can see that it could be convenient if Prime would see the unit not as a real unit but rather as a simple factor in that case.
The symbolic processor is not aware of units and treats it as normal (unknown) variables. Consequently a symbolic evaluation works.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
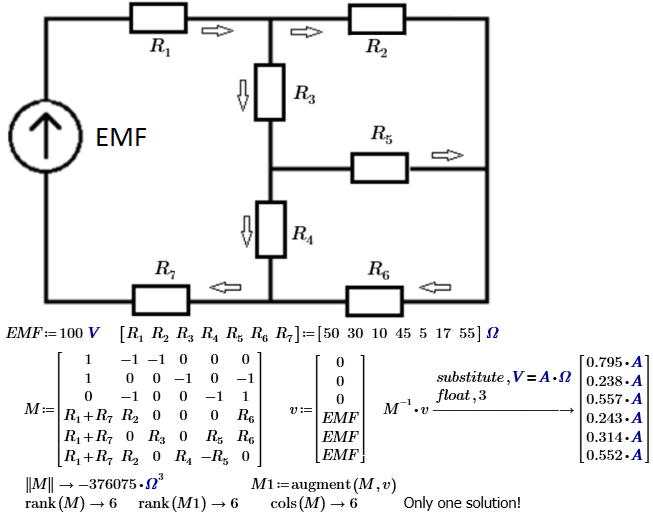
I think must be so (the system has infinity numbers of solutions) - Prime must have a new rank function.
(I think I am a first man of the World who try to calculate a rank of one mixed units matrix. ![]() )
)

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your routine can be written more compact using vectorization, but it (and yours) yields wrong results in some (not so rare) occasions:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes! My routine is better for education
Matter of taste and in this case I tend to disagree.
But the critical point is that the routine (both) aren't correct. They yield wrong results as in my second example. They shouldn't give a correct result ("if m=Ohm then rank is 1, otherwise its 2") or at least fail in the secon example if the units don't "match". Writing the routine that way would require loops instead of vectorization anyway 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I hope we have correct rank and others same functions in Prime 4.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Units still are not fully supported throughout - see changing display units for single elelements of a matrix or, as here some functions like rank.
In urgent need you may use the attached, which, when numerically evaluated gives the appropriate error message if the units don't fit and which can be used to get the correct result with symbolical eval. Unfortunately we can't put the latter in a single function as the intermediate numeric evaluation (matrix M2) is needed to get the units correctly simplified an cannot be achieved inside a program, AFAIK.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Werner.
(I will try to create one correct system for this circuit with rank(M)=rank(M1)=number of unknowns)

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
I will try to create one correct system for this circuit with rank(M)=rank(M1)=number of unknowns)
I think must be so:
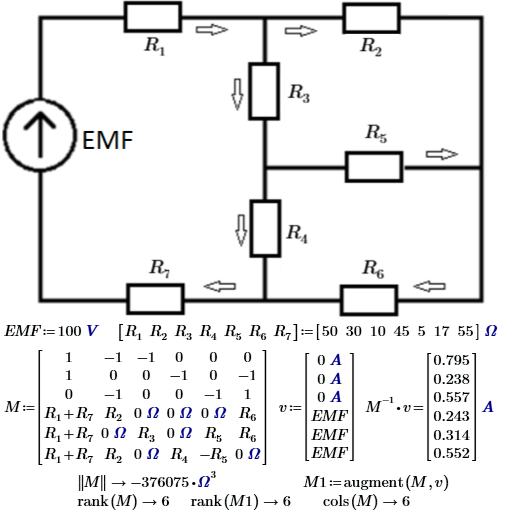
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solution:
But I think not all is correct in Prime! Jakov Kucan, where are yuo!?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As the symbolics is not aware of units its right.
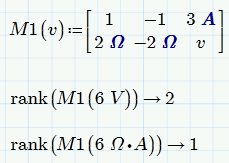
But using a modifier like "fully" I would have expected muPad to give me a more complete result by telling me, that the rank = 2 only if V is not Omega*A and its 1 otherwise.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
????? There are no zeros in my example.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Valery Ochkov wrote:
????? There are no zeros in my example.
I would like to point the others part of this discussion - 0A or 0, 0V or 0 etc. in symbolic and numeric math.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
I would like to point the others part of this discussion - 0A or 0, 0V or 0 etc. in symbolic and numeric math.
But I thought that Jakov explained that sufficantly - its the price we have to pay for dynamic unit checking which enables units of different dimensions in one matrix.
I think it should be no problem to consequently write 0V instead of just 0.






