Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Would someone help me in finding out how to solve an equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Would someone help me in finding out how to solve an equation
Hi all, I want to use symbolic solver to convert a fourth order equation to the multiplication of two second order terms. All variables are real numbers. I defined the equation like this but Mathcad showed no solution for it.

I attached the complete source code of Mathcad here. A big portion of this worksheet is the derivation of the left hand side of the equation, so you can simply ignore it (unless some of them are not executed by mathcad successfully). Would someone advise what is wrong with my solution? Can I put more restrictions in Mathcad, such as assume k0,k are real, to figure this out?
Many thanks!
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Don´t know if is useful, but this is the numeric solution. Obviously, must to make good guess for each alpha.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can greatly simplify the equations you are trying to solve. See the attached. Also note that you have no multiplication operator between k0 and the left parenthesis, which makes k0 a function name. I assume that's a mistake.
Fixing the above will not help though. k^2 appears in the numerator and in the denominator, so you have a fourth order polynomial in k. There is no symbolic solution for that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Richard, thank you for your advise! I did find a mistake from my side in defining k0, but the existing of it is correct. I am trying to solve alpha*s^4=s^4/(k0^2*wn1^4).
Do you think putting any limitation will help in solving this problem? For example. can I define k is much larger than 1? In control system, to separate two poles, we generally want to separate k*wn1 and wn1/k in frequency domain. Would you suggest can I do it? Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well, I made a mistake too. I made some changes, and forgot to put the variables back on the left hand side of the equations. Here's an update. It doesn't change the conclusion though.
Hi Richard, thank you for your advise! I did find a mistake from my side in defining k0, but the existing of it is correct. I am trying to solve alpha*s^4=s^4/(k0^2*wn1^4). Do you think putting any limitation will help in solving this problem? For example. can I define k is much larger than 1? In control system, to separate two poles, we generally want to separate k*wn1 and wn1/k in frequency domain. Would you suggest can I do it? Thank you!
I'm not sure I quite understand your corrected equation, since you have s^4 on both sides, which will just cancel.
Regardless, there is no symbolic solution for a fourth order polynomial. Why do you need to solve this symbolically? Finding the solution numerically is almost certainly possible, and much easier.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
Regardless, there is no symbolic solution for a fourth order polynomial.
?

There is a symbolic solution for a fourth order polynomial, above is a part.
Or am I missing something?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I stand corrected. I could swear that I read somewhere that there was no symbolic solution for polynomials of order higher than three. Now I look into it a bit more, it turns out that there is not only a solution for a fourth order polynomial, but someone figured it out several hundred years ago ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So what you want is:
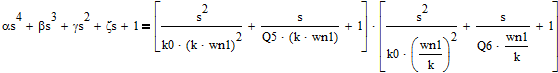
And now you want to express k0, k, Q5 and Q6 (and NOT wn1...!) in terms of the greek letters.
OK. Expansion of the right-hand-side gives:
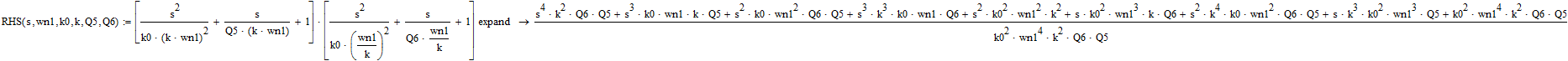
for which we can find the coefficients:


and finally we find:
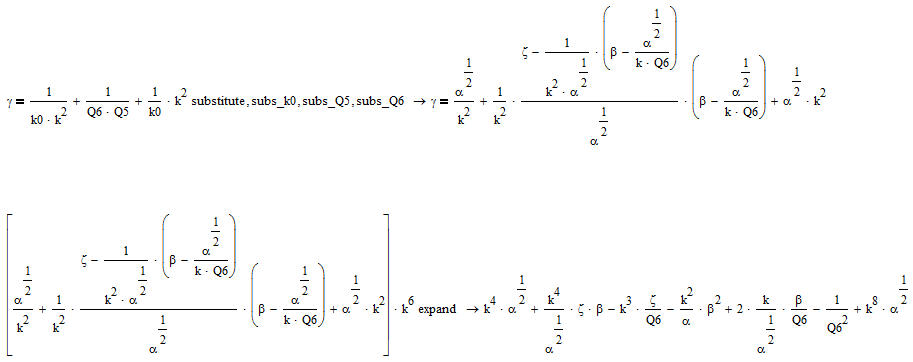
which means that to find k we have to solve an 8th order polynomial symbolically.
I guess that's a bit too much.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Yuhang. I can't get a solution with those assumptions.
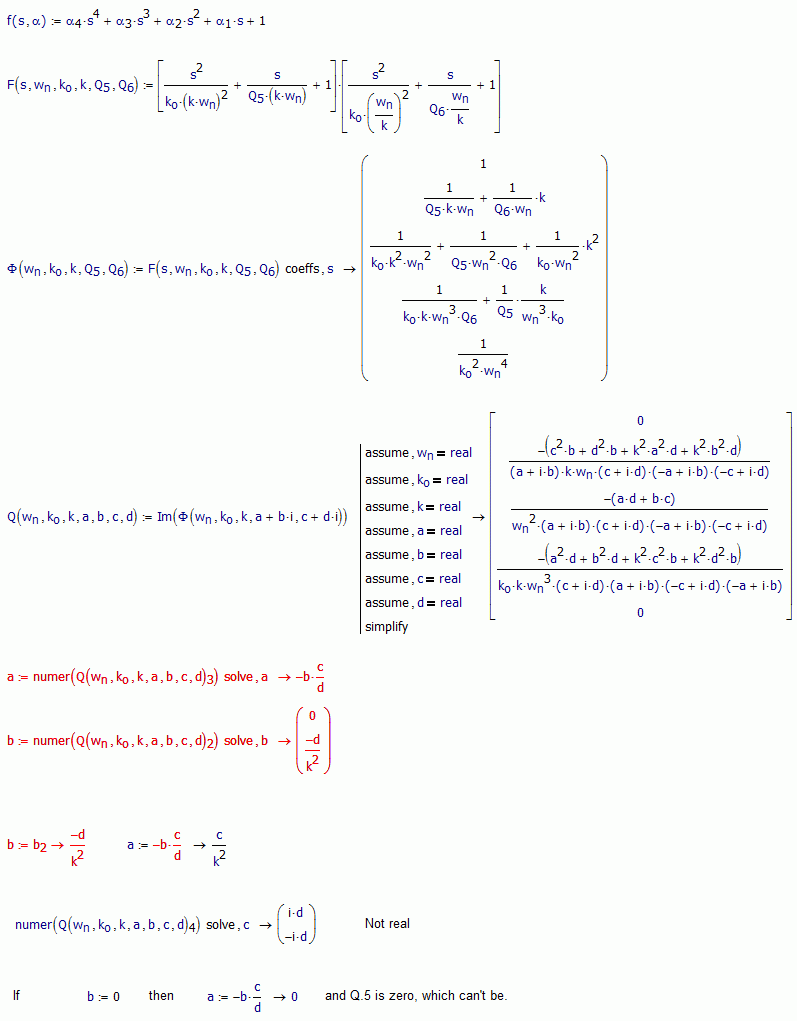
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Alvaro, thank you so much for your help! I am trying to follow your pattern to see what I can do in my original worksheet, but got the problem in putting the line after the ":=" equation (the one above the red texts in your picture). Would you advise me how to can use "Add line" command to put it after the Q():=Im(Phai()) ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Yhuang. I use mc11, and don't have any prime version (yet, probably next week), but in this old version is with Ctrl+Shift+Dot. Maybe any other collab can give you an actual answer.
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Alvaro.
Long time no see ![]() . What brings you back?
. What brings you back?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Richard. A lot of work at the university. Have some few days, and maybe, new mathcad prime too. Thanks for your message.
Have a very nice mounth!.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your Prime license is also good for the latest release of Mathcad 15, which in most ways is still superior to Prime. So be sure to install that too ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm sure we all look forward to you being Primed and ready for action again, Alvaro! ![]()
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot Stuart. A plasure reading you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Prime, insert the symbolic evaluation operator from the toolbar or using Ctrl +. There is a placeholder above the operator. Put the cursor in that and add the keyword. To add another keyword either type a comma (to get a horizontal list of keywords) or use Shift Enter to get another line.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi LucMeekes, thank you so much for this investigation. I will follow your worksheet to see if there is any improvement I can make!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Don´t know if is useful, but this is the numeric solution. Obviously, must to make good guess for each alpha.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Alvaro, thank you so much! I have a last question related to a long expression.
Like one coefficient shown above, if Mathcad returns a long expression, like a+b+c+d+......, how can I convert it to have a easier looking? I want to express it as
a
+b
+c
+d
....
Would you tell me how can I do it? Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In version 15 or before:

instead of "+", "shift,enter"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Fred, that works! I have another question to you. In the first post in this thread, I upload it a worksheet. The coefficient of s^2 did not show because it is too long. If I want to show it, how can I let Mathcad display it, (preferably the compact looking like what you taught me). Thank you!






