Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Community
- Creo+ and Creo Parametric
- 3D Part & Assembly Design
- Drawstring bag design
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Drawstring bag design
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Drawstring bag design
Folks
i need help modeling a drawstring bag in its relaxed and compressed position. I figured the top section can be modeled using trajpar or helical sweep. The bottom with surfaces and will connect together using merge, trim, etc. Would anyone share a cad model that resembles this
thanks
- Labels:
-
General
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
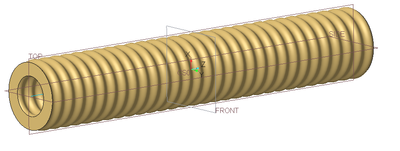
Here's a quick idea. First is a Curve from Equation with a cylindrical coordinate system. Equation:
theta = t*360
z = 0
r = radius+sin(t*360*20+90)*variance
I used radius 50 and variance 5 for my example. I use parameters for these, as I'll explain below.
Adapt measurements as needed. Inside is a circular sketch which is only used as the sweep origin. Lower down, there's an oval sketch. Make a surface-only variable section sweep connecting a line between the wiggly line and the oval. Make sure to use the circle as origin, so the sketch doesn't change angle as it goes around.
Then I made a single line further down, and connected it to the side surface with a tangency requirement and mirrored that.
Finally merged it all and made a round to make it less pointy at the bottom. Then thicken. You could play around some more if you want a different shape below. Result as above.
I then made a family table controlling the radius and variance. I increased the radius to 80 and set the variance to 0, which gives you a nice circular opening to show an open version of the bag. Result as below.
It's not super pretty, but it's a quick job. If you want it more realistic-looking, the Freestyle tool might be your best bet. Sorry, can't upload the part from here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Pettersson
Is the origin sweep superimposed on the equation (wiggly) curve? In the VSS, i tried to sketch the section as a vertical line between the origin-oval and as well the equation-oval and it produces a cone. In VSS, whats the section looks like?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
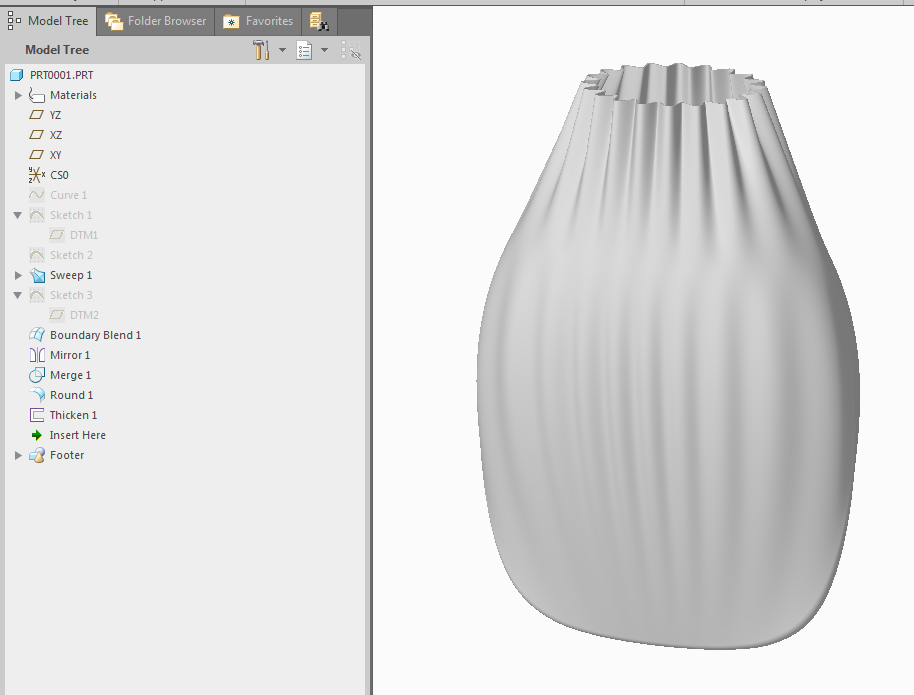
There are three sketches: the equation, the origin (a circle) and the oval. When making the VSS, select the origin first, then the other two. Then draw a straight line from the equation curve to the oval. The origin isn't really part of the sweep; it's just used to set the normal direction of the sketch. Therefore it doesn't matter where it's placed or how big it is; it just needs to be a perfect circle. Hope that helps. I can't upload a part, but here are some screenshots.
In the final two, instead of a straight line, I did a spline and constrained it to being vertical at the oval. This stops the ripples from propagating into the boundary blend.