- Community
- Creo+ and Creo Parametric
- 3D Part & Assembly Design
- Equations for Curves (and more)
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Equations for Curves (and more)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Equations for Curves (and more)
I wish I had found a list like this a few years ago. I've searched the web and compiled the following list for your enjoyment. Many are probably considered basic with a few very cool, complex curves thrown in. The list is divided into the coordinate systems that you will have to choose when creating the datum curve.
To initiate the command that will allow you to try these, go to Insert>Model Datum>Curve>From Equation.
![]() After the Equations section see the section title Links to find PlanetPTC discussions and videos that have demonstrated and, in some cases, explained the curve from equation command in more detail with ways to incorporate relations and parameters.
After the Equations section see the section title Links to find PlanetPTC discussions and videos that have demonstrated and, in some cases, explained the curve from equation command in more detail with ways to incorporate relations and parameters.
![]() Attached is a Creo Elements/Pro 5.0 part file with all of the equations included.
Attached is a Creo Elements/Pro 5.0 part file with all of the equations included.
In the comments, please share any equations or links that you know. Other suggestions are welcome, too.
EQUATIONS
Cartesian Coordinates: x, y, & z
The z variable is not necessary, but when used will give the curve that extra dimension. If in doubt, try z = t*10.
Sine
Cartesian coordinates
x = 50 * t
y = 10 * sin (t * 360)
Rhodonea
Cartesian coordinates
theta = t * 360 * 4
x = 25 + (10-6) * cos (theta) +10 * cos ((10/6-1) * theta)
y = 25 + (10-6) * sin (theta) - 6 * sin ((10/6-1) * theta)
Involute
Cartesian coordinates
r = 1
ang = 360 * t
s = 2 * pi * r * t
x0 = s * cos (ang)
y0 = s * sin (ang)
x = x0 + s * sin (ang)
y = y0-s * cos (ang)
Logarithmic
Cartesian coordinates
z = 0
x = 10 * t
y = log (10 * t +0.0001)
Double Arc Epicycloid
Cartesian coordinate
l = 2.5
b = 2.5
x = 3 * b * cos (t * 360) + l * cos (3 * t * 360)
Y = 3 * b * sin (t * 360) + l * sin (3 * t * 360)
Star Southbound
Cartesian coordinate
a = 5
x = a * (cos (t * 360)) ^ 3
y = a * (sin (t * 360)) ^ 3
Leaf
Cartesian coordinates
a = 10
x = 3 * a * t / (1 + (t ^ 3))
y = 3 * a * (t ^ 2) / (1 + (t ^ 3))
Helix
Cartesian coordinates
x = 4 * cos (t * (5 * 360))
y = 4 * sin (t * (5 * 360))
z = 10 * t
Parabolic
Cartesian coordinates
x = (4 * t)
y = (3 * t) + (5 * t ^ 2)
z = 0
Eliptical Helix
Cartesian coordinates
X = 4 * cos (t * 3 * 360)
y = 2 * sin (t * 3 * 360)
z = 5
Disc Spiral 1
Cartesian coordinates
/* Inner Diameter
d = 10
/* Pitch
p = 5
/* Revolutions
r = 5
/* Height; use 0 for a 2D curve
h = 0
x = ((d/2 + p * r * t) * cos ((r * t) * 360))
y = ((d / 2 + p * r * t) * sin ((r * t) * 360))
z = t * h
Butterfly
a=cos(t*360)
b=sin(t*360)
c=cos(4*t*360)
d=(sin((1/12)*t*360))^5
x=b*(exp(a)-2*c+d)
y=a*(exp(a)-2*c+d)
Fish
a = cos (t * 360)
b = sin (t * 360)
/* As "c" increases the fish gets fatter until it transforms into a figure 8.
c = 10
x = (C*a-20*((b)^2)/1.5)
y = c * a * b
Cappa
/* "c" is a scaling variable
c=20
/* Revolutions
r=1
/* Height
h=0
x=c*cos(t*r*360)*sin(t*r*360)
y=c*cos(t*r*360)
z=t*h
Star
/* "a" & "b" are scaling variables
a=2
b=2
/* If, r=2/3 ----> astroid
/* If, r=2 ----> ellipse; when a=b, its a circle
/* r cannot equal 1
r=2/3
x=a*(cos(t*360))^(2/r)
y=b*(sin(t*360))^(2/r)
z=0
Bicorn
/* "c" is a scaling variable.
c=5
a=cos(t*360)
b=sin(t*360)
x=c*a
y=c*(a^2)*(2+a)/(3+b^2)
Talbots
/* "c" is a scaling variable.
c=10
a=cos(t*360)
b=sin(t*360)
x=C*a*(1+exp(2)*(b^2))
y=C*b*(1+exp(2)*(b^2))
Cylindrical Coordinates: r, theta, & z
Spiral
Cylindrical coordinates
r = t
theta = 10 + t * (20 * 360)
z = t * 3
Circle Spiral Column
Cylindrical coordinates
theta = t * 360
r = 10 +10 * sin (6 * theta)
z = 2 * sin (6 * theta)
Helical Wave
Cylindrical coordinates
r = 5
theta = t * 3600
z = (sin (3.5 * theta-90)) +24 * t
Basket
Cylindrical coordinates
r = 5 + 0.3 * sin (t * 180) + t
theta = t * 360 * 30
z = t * 5
Disc Spiral 2
Cylindrical coordinates
R = 50 + t * (120)
Theta = t * 360 * 5
Z = 0
Apple
Cylindrical coordinates
a = 10
r = a * (1 + cos (theta))
theta = t * 360
Spherical Coordinates: rho, theta, & phi
Butterfly Ball
Spherical coordinates
rho = 8 * t
theta = 360 * t * 4
phi = -360 * t * 8
Spherical Helix
Spherical coordinates
rho = 4
theta = t * 180
phi = t * 360 * 20
UFO
Spherical coordinates
rho = 20 * t ^ 2
theta = 60 * log (30) * t
phi = 7200 * t
Unnamed
Spherical coordinates
rho = 200 * t
theta = 900 * t
phi = t * 90 * 10
LINKS
Peruse the links for more equations and explanations as to how they work.
Web Links
- Involute Gears
- Power Tools: Curves by Equation
- This gives details about using Pro/E dimension references in the equation to give it a parametric touch.
Links to curve-from-equation Discussions on PlanetPTC:
- Curve from Equation Sample for Newbies
- Capto
- How to Create a Curve from the Equation? Does Anybody Know?
- Datum Curve from Equation Driven by Parameters
- Constant Force Spring Model
- Involute Helical Gear Geometry
Links for related PlanetPTC content:
If you think curves from equations are cool, then the following is right up your alley. These delve into the use of variable section sweep and the trajpar variable.
- From E-learning with Vladimir Palffy
- Fun with Helical Sweeps and Trajpar
- Conch Shell in Creo Parametric
- How to Create Twisted Wires
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice find! thanks for posting it.
Note: I suggest downloading by using the "View as PDF" button in the "Actions" menu in the upper right of this page. That way you can cut & paste and try some out. Interesting stuff here. Not a whole lot of practical applications in most cases (except involutes, etc.), but very cool for fun.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, the models that you shared with me lead me to create this document. I haven't yet figured out how to recreate your models, but I have rediscovered my interest in the curve from equations command. However, I am aware that you used a different method to create your geometry. Maybe (or, hopefully) you'll share it with us later.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm kind of waiting to see if someone from PTC can't tell me how some of them, in particular, the wavy-washer, 3rd_curve and the coiled_spiral were created. ![]() How did I get the trajectory in the latter to circle back on itself 4 times without failing?
How did I get the trajectory in the latter to circle back on itself 4 times without failing? ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the post Kevin. I actually have a couple to add to your list. I discovered one really cool equation while trying to help someone else on Planet PTC> I haven't gotten a chance to write it up yet so I haven't posted it. When I do I'll send it to you, too so you can include it in your document (if you'd like).
Thanks!
-Brian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I absolutely want them and will add them to the document. That goes for everyone. In time, I think I will also add images for each curve so a user, without having to try all of them, could decide which one they want to experiment with.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
l = 2.5
b = 2.5
x = 3 * b * cos (t * 360) + l * cos (3 * t * 360)
Y = 3 * b * sin (t * 360) + l * sin (3 * t * 360)
I have a question about the Double Arc Epicycloid. I'm looking to make a 4 arc version. Based on your equation, the (3 * t * 360) would change to (5 * t * 360). What I'm unclear about is the rest of the formula. The basic formula to create a epicycloid is:
x = (R + r) cos theta - r cos ((k + 1) theta)
y = (R+ r) sin theta - r sin ((k + 1) theta)
Where R = radius of the circle being revolved around, r = radius of the circle revolving around the R circle and k = the number of arcs.
What does "l" and "b" stand for in your equation? It looks like "l" stands for the "r", but I'm not sure about the "b". Also, what is the 3 shown before the "b" supposed to stand for?
The outside diameter at the tangent points of the arcs for my project is .7874 (or 2 cm).
Also, do you have a formula for creating a hypocycloid?
Thanks.
brian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
These equations aren't my own, but I can shed some light on them with the caveat that I don't have access to Creo and the equations anymore--If I did I could answer your questions better.
Anyway, the l & b from the equation are just multipliers, if I remember correctly. In order to maintain the desired shape of the curve, I think the intention was to only change the l & b values, thereby modifying the size of the curve, yet still being able to call it a double arc epicycloid. Because if you change the other values then the shape no longer deserves that name (I think). Did I make any sense?
Brian or Frank, from the posts above, may be able to help more.
Thanks for replying. It's a fun feature to play around with.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First, it would help if I posted the equation correctly.
x = r (k+1) cos theta - r cos ((k+1) theta)
y = r (k+1) sin theta - r sin ((k+1) theta)
Anyways, I figured out that both "l" and "b" are both the same representation of "r". Changing them to the value I needed and changing each of the 3's to 5's (which is the k+1 value) made it work. Thanks for the input.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
hello!
I would deeply appreciate your help, as I am new to inserting equation into Pro E.
What is the cartesian or cylindrical equation for Logarithmic spiral that I should enter to the ptogram?!?!?
below the equation
http://mathdl.maa.org/images/upload_library/23/picado/seashells/espiraleng.html
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Greetings,
I've been trying to turn the following into a functional epicycloidal curve from equations but have hit a wall:
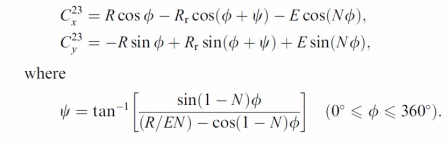
I've reduced it to the following after trying it in its original format but it still blows up at zero, rotates the epicycloid CCW 5° or so and generally isn't the correct curve. This request for help may be beyond the scope of this forum in which case I'd be willing to talk consulting terms. Thank you.
A = 90
B = 12
C = 11
D = 3
x = A*cos(t*360) - B*cos((t*360) + atan ((sin(1-C)*(t*360)) / (A/(D*C) - cos(1-C)*(t*360)))) - D*cos(C*(t*360))
y = -A*sin(t*360) + B*sin((t*360) + atan ((sin(1-C)*(t*360)) / (A/(D*C) - cos(1-C)*(t*360)))) + D*sin(C*(t*360))
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks lot finally i got about the equation for curves
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
do you know whether it is possible to split the range of t into multiple intervals?
for example I would like to set:
for 0<t<0.5
x=0
y=t
for 0.5<t<1
x=t
y=t^2
I would really need this because if I build these two pieces with two separate curves and then merge them with the "Copy - evaluation" command, any sketch projecting the unified curve will always see it as two separate pieces and this causes me problems in sketch references when the curves themselves change.
thanks
bye
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Short answer, no. You can create the IF statements for the different ranges but they do not get evaluated correctly.
Long answer from PTC:
"The relation for trajpar does not support ranges (changes of function on different pieces of the trajectory, implemented with 'if' statements). Suggested using multiple variable section sweep features, with family tables, or defining geometrical breaks in the trajectory."
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not really sure what's "Copy - evaluation" command, but try searching for a term "Composite curve".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Tom,
thanks for your tip. What do you exactly mean with "they do not get evaluated correctly"?.
Also, how could I define geometrical breaks ? by trimming the curve?
bye
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello James,
with Copy-Evaluation I was meaning the action of selecting the curve (which highlights in green), Ctrl+C, then Ctrl+V and the copy evaluation menu opens (where you can add more curves to the copied one).
Bye
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What do you exactly mean with "they do not get evaluated correctly"?
Well, I'm not a developer but from what I can tell the curve generator dynamically adjusts how many locations it needs to evaluate 't' for based on the results of the previous evaluations. It will progressively reduce the step size (down to some minimum) until it meets some type of fitting criteria. I don't know the exact algorithm, but if the first section of the curve uses an equation that makes it flat, then the entire curve will end up flat, regardless of what the equation for the other sections might be.
how could I define geometrical breaks ? by trimming the curve?
Yes, exactly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
Thank you so much for your web site
I want to plot NACA Aifoil by this equation but I can not view the Cure in PTC Creo Parametric?!
M=0.08
a0=0.2969
a1=0.126
a2=0.3516
a3=0.2843
a4=0.1015
T=0.12
p=0.4
x=t-((T/.2)*((a0*t^.5)-(a1*t)-(a2*t^2)+(a3*t^3)-(a4*t^4)))*(Sin(360*atan((M/p^2)*(2*p-2*t))))
y=((M/p^2)*(2*p*t-t^2))+((T/.2)*((a0*t^.5)-(a1*t)-(a2*t^2)+(a3*t^3)-(a4*t^4)))*(Cos(360*atan((M/p^2)*(2*p-2*t))))
z=0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
M=0.08
a0=0.2969
a1=0.126
a2=0.3516
a3=0.2843
a4=0.1015
T=0.12
p=0.4
x=t-((T/.2)*((a0*t^.5)-(a1*t)-(a2*t^2)+(a3*t^3)-(a4*t^4)))*(Sin(atan((M/p^2)*(2*p-2*t))))
y=((M/p^2)*(2*p*t-t^2))+((T/.2)*((a0*t^.5)-(a1*t)-(a2*t^2)+(a3*t^3)-(a4*t^4)))*(Cos(atan((M/p^2)*(2*p-2*t))))
z=0





