Skip to main content
S
SYNDAKIT15-Moonstone
15-Moonstone
February 25, 2021
Question

Help writing a relation for a bend

  • February 25, 2021
  • 1 reply
  • 2328 views

I cant' figure out the correct equation to drive the wing outside diameter and wing inside diameter for this part. 
(I will attach the part file)

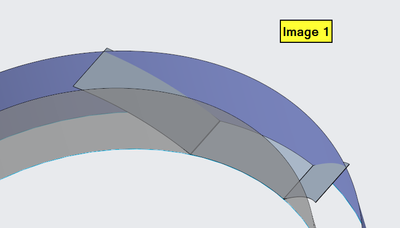
Image 1 - This is the part bent. The part wings should be fitting into the vertical surface walls. 

SYNDAKIT_0-1614269929351.png

 

Image 2 - Just for a visual reference.

SYNDAKIT_1-1614270149185.png

 

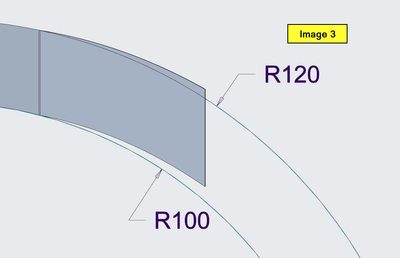
Image 3 - View showing that the bent wing is falling outside of the inside and outside radius. (It should be inside of them)

SYNDAKIT_2-1614270262298.png

 

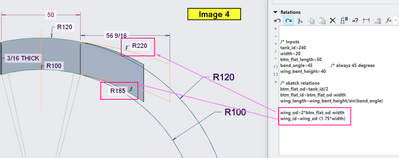
Image 4 - View showing the sketch and relations driving the part.

SYNDAKIT_3-1614270319890.png

 

 

 

 

I'm open to other methods as long as I can flatten it and that the flat pattern drawing will let me place dimensions on the arcs.

 

Thank you for your help

1 reply

tbraxton
22-Sapphire II
tbraxton22-Sapphire II
22-Sapphire II
February 26, 2021

Here is a model that has the wings constrained as specified. In order to get this the bend lines need to be normal to the radial surface of both surfaces making the ID and OD. This was built with no relations, it was all done with geometry constraints. This is a quick hack to get the geometry to regenerate for reference.

 

tbraxton_0-1614298018028.png

 

    S
    SYNDAKIT15-MoonstoneAuthor
    15-Moonstone
    March 1, 2021

    Thank you Tbraxtn. 

    That is a really clever method. 

     

    That model get's me really close to what I'm trying to achieve. There is one other hurdle I need to get over though, and that's the dimensioning part. When I go to dimension the flat pattern,  I would like to be able to pull a radial dimension for the wings; although because of the geometry this may not be possible.

     

    And that brings me back to the relations. I thought that if I started with a sketch that uses radius dimensions for the wings and was controlled by relations, that then when I did the flat pattern I would be able to pull radius dimensions again. 

     

    If I'm unable to figure out a way to get the relations to work, I might just have to fake the radius dimension by creating a sketch that's constrained to the spline of the flat pattern at three points; the two ends and a mid point:

    SYNDAKIT_0-1614607122584.png

     

    What are your thoughts?

     

    Thank you for helping me out.
     

     

     

     

     

    tbraxton
    22-Sapphire II
    tbraxton22-Sapphire II
    22-Sapphire II
    March 1, 2021

    The wing curved edges are not constant radius so there is no single radius dimension for these curves. If you observe the equation (or shape) of the curve created by the intersection of a plane and a cylinder which is in the context of your design then you will see the nature of the curve. It is an ellipse so you can define it in the flat pattern with the major and minor axis along with the conic parameter.

     

    Consider the intersection of a plane at angle of 45 degrees relative to the base of a right cylinder (the wings) and you will see that it is an ellipse that is the result of the intersection. You can derive the parametric equation of the ellipse analytically and use that in relations to define the flat pattern if desired. In the interest of expediency I would sketch the ellipse on the plane of unbending such that you have access to the dimensions of the ellipse for the drawing. Make sure to use the conic parameter for an ellipse when sketching in Creo.

    Terms & ConditionsAccessibility statement