- Community
- Creo+ and Creo Parametric
- 3D Part & Assembly Design
- Re: How to create a datum plane normal to an axis ...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to create a datum plane normal to an axis and tangent to a sphere
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to create a datum plane normal to an axis and tangent to a sphere
Hi All,
I have a sphere and an axis passing through that sphere. I want to create a datum plane such that it is normal to this axis and tangent to the sphere. Creo 3.0 won't allow me to select the axis and the surface at the same time. Am I missing something?
Thanks
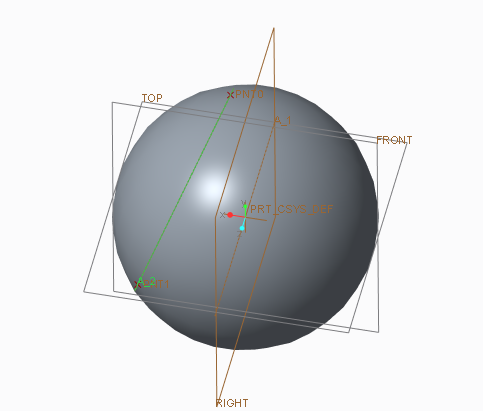
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
An idea... Select the axis, create the plane, define it normal then select the surface and define it tangent.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I just tried my idea... it's not working ! ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
The axis doesn't pass through the centre of the sphere. tangent and normal to axis can only be selected if the axis passed through the centre of the sphere.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for replying!
Unfortunately in my case the axis doesn't pass through the center.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think one of the troubles is that there are actually two solutions for the mathematical problem. The resultant plane may lie on either "side" of the sphere. Also, I've found the tangency constraint for these types of situations to be really flaky. The type of thing where it shows me the "correct" (expected) solution, but once I accept, the plane is on the other side of my geometry, etc. You might be forced to create a point at the desired side of the sphere and use that and the axis to define the plane.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your answer!
I actually have a part of the sphere which is less than a hemisphere. So mathematically there should be only one plane which is tangential.
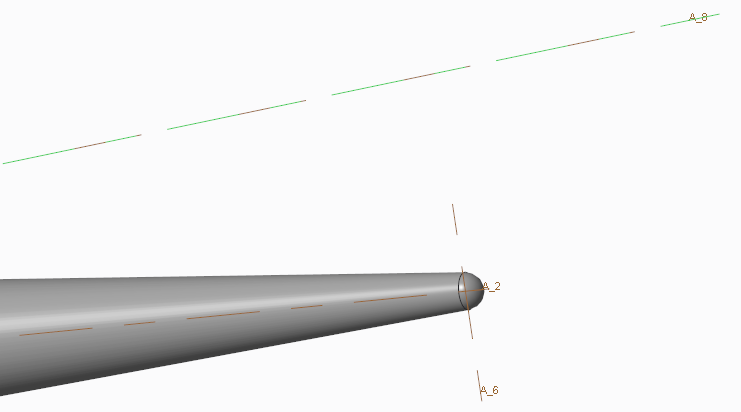
I want a plane normal to A_8 and tangential to the spherical tip.
I was hopping to avoid creating a point on the surface as it would mean a lot of geometrical calculations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I know this isn't the "Magical" answer your looking for, but I don't know how your gonna get where you want to go without additional construction geometry.
In this case, I would Sketch a curve... Normal to A_8 and Tangent to your dome...
Then create your plane Through the sketch curve, and Normal to A_8.
Good Luck
Bernie
Bernie Gruman
Owner / Designer / Builder
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think the problem is the way Creo creates the geometry. From what I can tell it creates the sphere as a blend surface. I think Creo only allows the tangent constraint to be used with cylindrical surfaces.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems there are significant limitations for using spherical surfaces as datum entity "tangent" references. Quick investigation shows that points can be constrained to be "on spherical surface", or to be placed at the center of spherical surface, and an axis can be constrained to be "normal" to a spherical surface. But there doesn't seem to be a concept "tangent" to a spherical surface; tangent seems to be valid only as related to cylindrical surfaces.
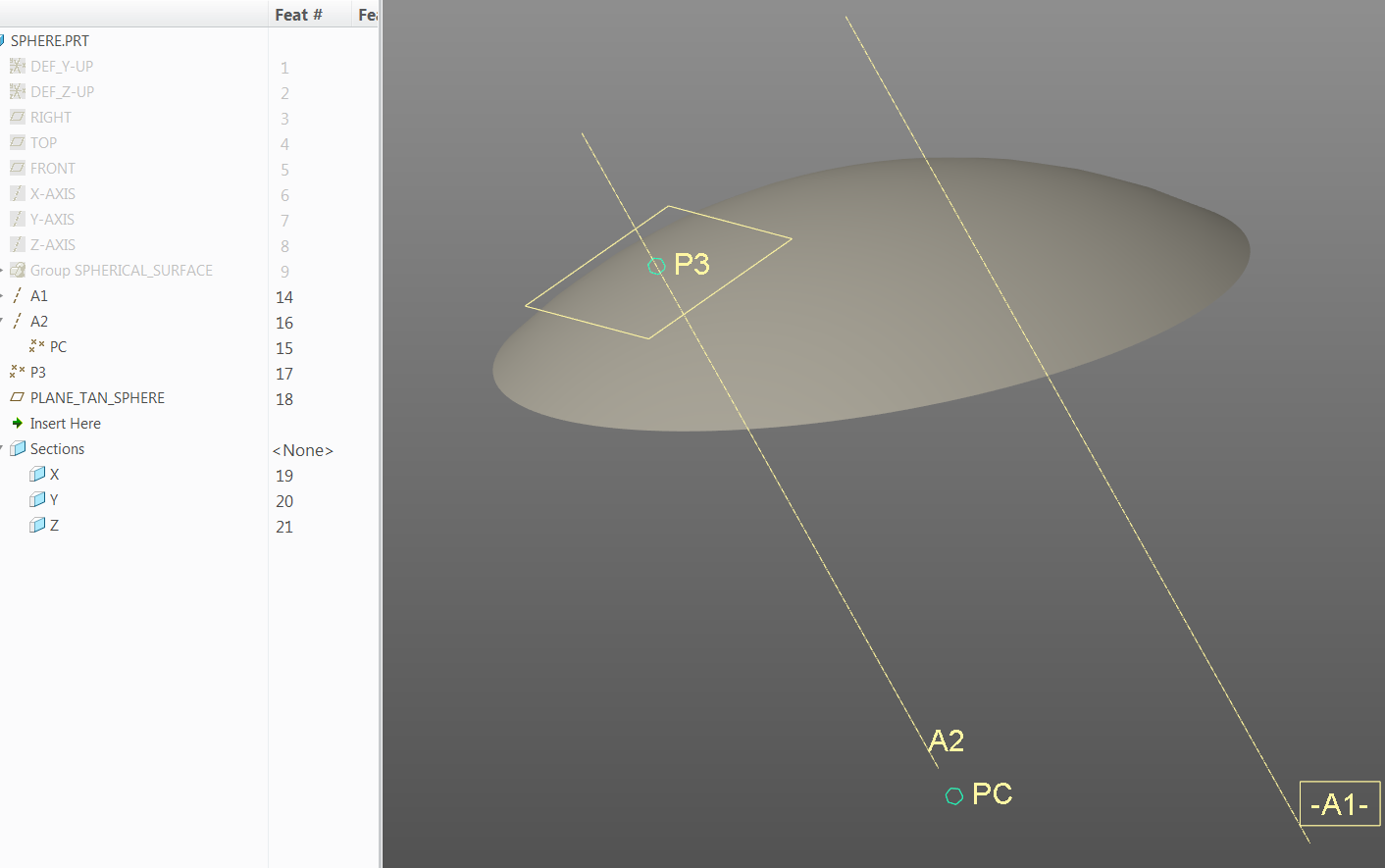
Anyway, you can get what you want by using points, planes and axes entities:
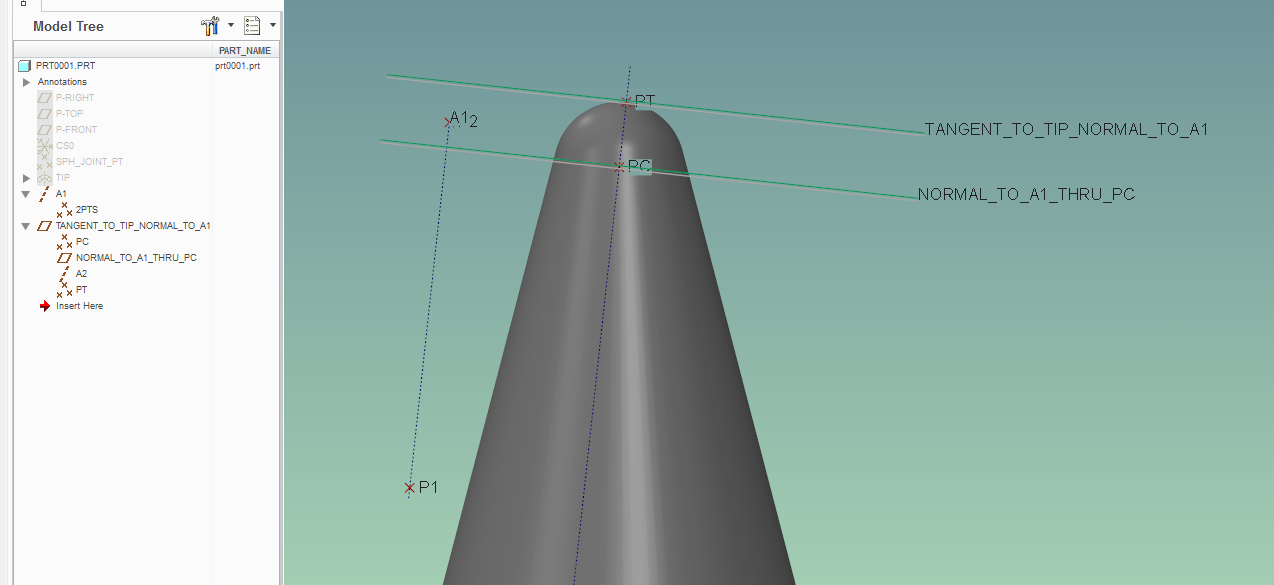
Given axis A1 that goes through datum points p1 and p2 (like your axis A_8).
You will need a point PC that is at the center of the tip; you can make it by creating a datum point and select the spherical surface, and use the "center" option.
Then, you can create a plane normal to A1 and through PC.
Then, you can create an axis A2 that goes through PC and is normal to the plane "NORMAL_TO_A1_THRU_PC"
This lets you get the tangent point PT - it is a point on the spherical surface and on the axis A2.
So finally, you get your plane that is through PT and normal to A1
All these construction datums can get "absorbed" into the datum plane feature so your model tree is kept clean.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
[edit] It's good to be able to construct relationships like this. while it's true, the sphere isn't very flexible for using as a datum in this way, the fact is I wouldn't' want to in the first place. It's much better to define your constraints so that there is actually only one solution. People bitch about creo doing funky things when they define patterns or want to adjust their sketch and it blows up. The simple fact is - it's not creo, it's the constraints. ambiguous constraints lead to ambiguous solutions. So back to the point - it's better to construct a as unambiguous a solution as you can. Or at least to understand the ambiguity to recognize it when things fail (so you can fix it)
And this problem right here - this is one of the uses of that high-school geometry class 😉 yay!
--------------------
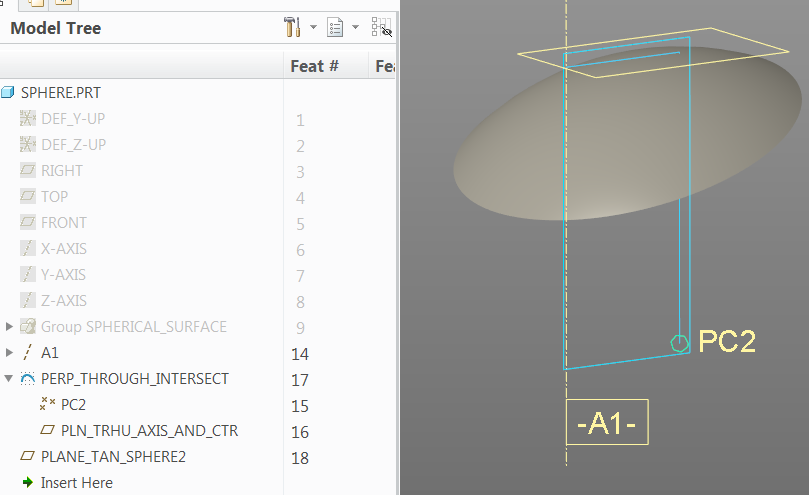
Slight optimization of the above. just define the axis parallel to the original axis through the center.
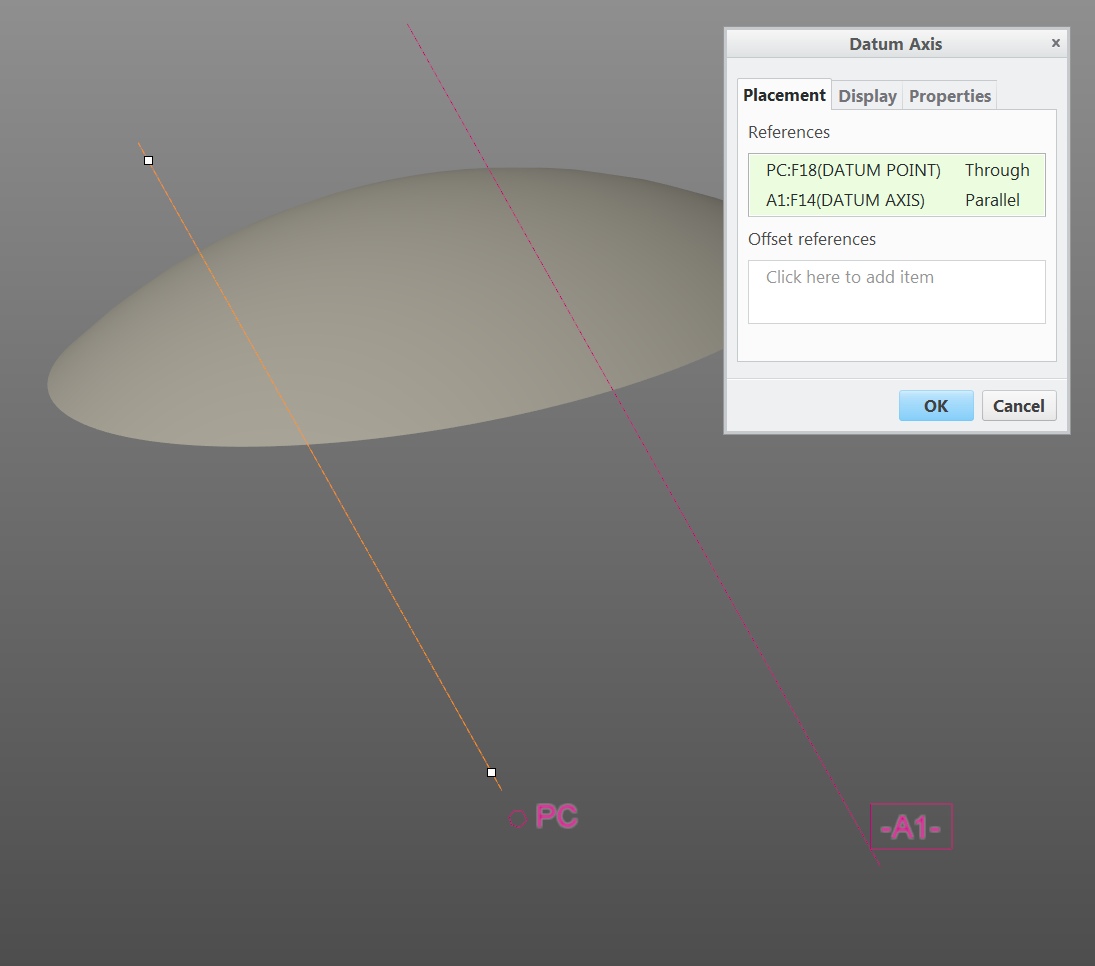
And another way to do it would be to create a datum plan through your arbitrary axis and the center of the sphere. you can then use an xsec ref and draw a line from the center to the surface of the sphere, and then perpendicular to that, and the original axis, you can draw a line that is implicitly tangent to the sphere.
then it's trivial to create a datum plane normal to the original axis and through the line-segment that is tangent to the sphere.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You want to make the plane - normal to A_8 and tangent to sphere ??
1. first of all, Make the plane(DTM1) normal to A_8 (anywhere)
2. Make the plane that you want (DTM2)
- select the DTM1 and set the option " parrarel"
- select the surface of sphere and set the option "tangent"
This is the way I know...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have you tried spherical coordinate system to define the plane?
And if not asked directly, the axis is normal to the sphere, right?
Otherwise there is no solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As I understood the question:
The solution is tangent to sphere, but not AT the point of intersection between sphere and axis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah! That opens up a few more possibilities.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A plane can only be made tangent to a surface if it is cylindrical or conical. You'll need to try another method to get the desired result.





