Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Community
- Creo+ and Creo Parametric
- 3D Part & Assembly Design
- Re: Spiral curve with uniform pitch
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Spiral curve with uniform pitch
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Spiral curve with uniform pitch
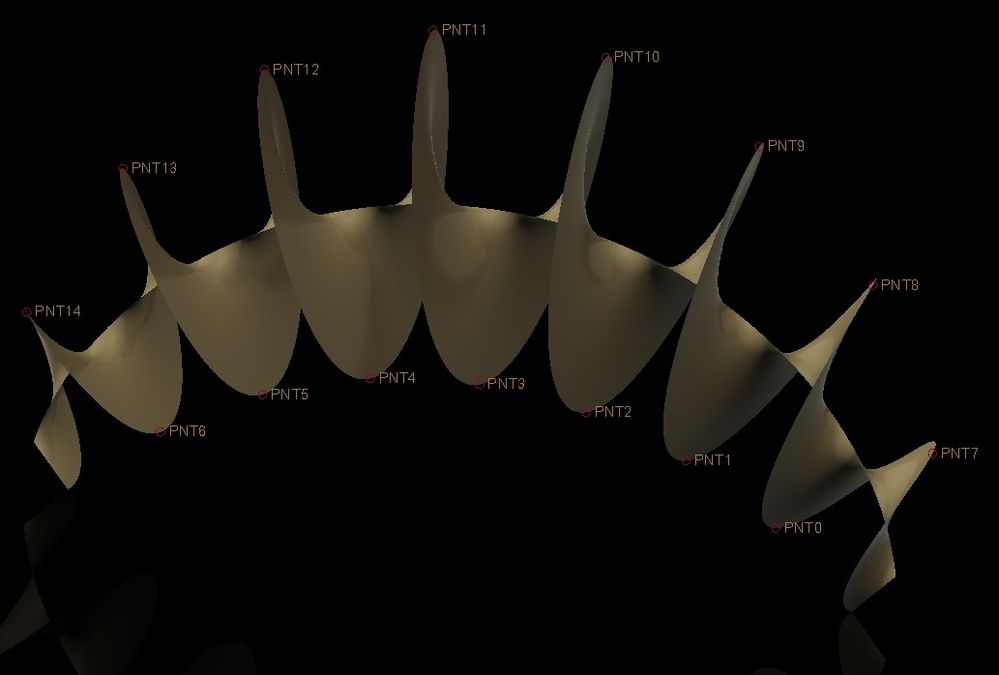
Hi, I am trying to create a spiral curve with uniform pitch along its sweep direction. It seems Creo is only able to control the pitch along its trajectory spine, nothing else. The pictures below show I am trying to create:
Creo4 part file attached here for your reference.
Anyone has any idea how do I achieve this ? Thanks
Solved! Go to Solution.
- Labels:
-
General
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
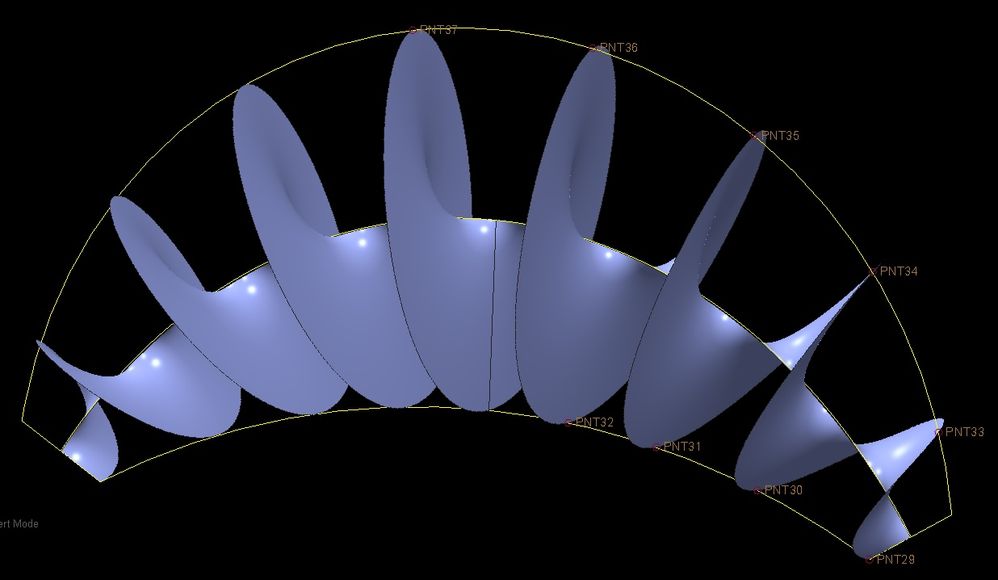
Ok, perhaps I was wrong-ish. I re-tried an earlier method with a tweak or 2. Actually simpler than the last one posted and a lot more like what you want. It MIGHT be possible to get it perfect, but I got as close as I think you can reasonably get, with the large arc, middle linear distance (from point to point) being about .030" different from the large arc end distance, with the others falling in the middle. The distances on the inner arc are exactly equal to 4 decimals. I don't think you can possibly realistically get closer. It's got a nice smooooth helix, which I like.
What's this for out of curiousity?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, I will try it out.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can't open the file since I'm on creo 3. In looking at the pictures instead of a model, I can;t tell what the cross section of the surface is, if it's circular or not. But, it looks like you can get CLOSE, but not quite what you want. Why? because the cross section of the helix is always going to be normal to the spine trajectory, when in reality you need it to change from one angle relative to the spine to another smoothly from one end, to the center, back to the angle at the start.
So, how exact does it need to be?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Also, even if you got it even closer, the pitch would ONLY be correct at the point where it intersects the 2 curves. The rotation of the spiral along the trajectory would have to be nowhere near linear to make it work...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
can you model it out and share. It's hard for me to understand from your description above. Thanks in advance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The base quilt was created using sweep and its cross section is circular along its spine (the middle curve). I would like to have uniform pitch along the sweep dir, as uniform as possible.
One idea i have is to generate a set of equally spaced points on the outer and inner curves using pattern, and join the corresponding points using datum curve on surface. I can then create the final spiral sweep using those curves. This method is tedious and hard to modify, not good.
What idea you have in your mind?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes you could put a ton of points on the surface, and approximate a true spiral, but that's not only tedious, but it'll give you a "spiral" that is not smooth. Also, you won't be able to force the curve onto the surface, you'd have to use that as a trajectory, and then do another intersection. Not good.
I'm assuming that the guiding curves shown are both TRUE arcs, and not some spline, conic, or ellipse?
I've got one more trick that didn't work the first time, but I'm going to try it a little differently this time.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you are a genius at programming with graph features driving the rotation of the spiral as it's being driven along the curves, are able to create a curve that exactly bisects the distance between the 2 curves to use as the spine trajectory (as I was able to do with some personal trickery), you MIGHT be able to do it, but as I said, the geometry simply does not work as you envision it, it simply CAN'T geometrically. The spiral would not be a smooth rotation, it would have to slow down, then speed up, then slow down again every 180deg of rotation to make the points on the intersecting plane that would give the even spacing at those points you show.
It was an interesting puzzle but one that, ultimately, really can't be solved in Pro/E (creo). Have fun with the file, and please pardon the extra curves, I wasn't able to quickly delete those. The quilt is the one I'm most happy with. Enjoy!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your effort. This is pretty good.Does it take a lot of work to create ? Do you mind to share the proe file?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The technique I used to create the spine that bisects the 2 different radius arcs I'm going to call a trade secret and won't divulge, but creating it is key, and is very easy actually but you have to think totally out of the box. I figured that the spine itself would be key to getting the spiral right....but how to create it from the arcs? I tried using one or the other as a spine, and the other as a trajectory and make the sketch line segment exactly 1/2 the distance between, and it didn't work because the section is always normal to either spine (either large curve or small curve), not normal to a constantly changing plane an equal percentage of distance down the trajectories. So, I did a modification of a trick I'd used before for different purposes and it worked perfectly. Then, I used the spine and both large and small arcs as trajectories, the sketch simply being a construction circle coincident to the "reference" (critical) points at the start of both the large and small trajectories. I did NOT align the center of the circle to the spine trajectory as it caused a slight distortion the first time I tried (opposite side of the second trajectory didn't touch the other arc), so, it was free to float with the circle making sure the cross-section of the spiral remained circular and both guide trajectories making sure the spiral always touched the guide trajectory arcs. Add a line from the center to the construction circle, with an angle dimension from the section centerline controlled by a section relation (in my case, d3 = TRAJPAR * 360 * 😎 and it's done.
If I may ask, what is this for?
Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok, perhaps I was wrong-ish. I re-tried an earlier method with a tweak or 2. Actually simpler than the last one posted and a lot more like what you want. It MIGHT be possible to get it perfect, but I got as close as I think you can reasonably get, with the large arc, middle linear distance (from point to point) being about .030" different from the large arc end distance, with the others falling in the middle. The distances on the inner arc are exactly equal to 4 decimals. I don't think you can possibly realistically get closer. It's got a nice smooooth helix, which I like.
What's this for out of curiousity?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks. I tried this out and it does work perfectly. My steps:
1. Sketch the spine section
2. add uniformly distributed points(at least 3) on the spine curve
3. Sketch the trajectory curve with reference to spine points to ensure it generates equally spaced points as well
4. sweep .
enclosed is the creo4 file.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
creo4 file.
The only issue I have with this method is that I am not able to sketch the outer section (bigger arc in this case) freely. The outer profile may be a spline curve instead of arc.
I encountered this problem when I tried modeling a spiral ring
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When you do the spinal bend, it's going to distort somewhat anyway, so, I wasn't going to worry about the larger arc not being perfect (you could probably take a ton of measurements and make it closer to perfect as a spline, but... - See EDIT:). My initial try worked at first....except then I realized that the resulting helix did not conform to the larger arc. So I shelved that approach, and did the other one. Then I realized I was an idiot, and went back to the spinal bend approach, but made the helix bigger, then used a swept surface on the bend to trim the helix perfectly. One thing I found, was that doing a "Lock Length" wasn't accurate enough, it left the helix a little short. So, I used that and the "Bend from the spine start to the selected reference" option as well and used a "datum on the fly" through the end to make the finished length right.
Oh, and I didn't use the points to drive anything, I added them afterwards at the intersection of the helix edge and the outer arc to measure the result. They were not needed to create the curves used.
Overall I'm happy with the result, glad I gave it one more spin, and think that's about as close as you'll ever get in creo. It was an interesting exercise for me.
If you think this was the solution, please acknowledge that and mark the thread closed, thanks.
Frank
EDIT: Just out of curiosity I made the larger arc a spline made of a bunch of points I measured.....and it didn't change the final result at all. This makes sense as the line elements are all normal to the spine, which in this case is a line, so trimming them isn't going to do anything to the "pitch" when you do the spinal bend and then trim the helical surface.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For some stupid reason, the first time I tried to do a simple sweep using just the 2 arcs it didn't work right. Turns out you don't need to do a spinal bend (though that obviously works). Yesterday I looked at it again and I was able to do it using the small arc as the spine trajectory (with section normal to that), and the larger arc as a guide arc and it worked fine. Obviously I had some option not set right.
Think it was just me not being too familiar with the new (to me) creo 3 interface. That saved from having to do a measure feature (old evaluate feature), simplified the layout, and removed a couple unneccessary features.
That just shows there are usually several ways to skin the cat.....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have tried out the graph option. I used a graph to control the rotating angle of the sweep section. The quilt created through this approach is quite close to what I wanted, see the attached pic for the graph section I used. However, the graph creation is not as easy as I expected it to be.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Perfect example of what I meant by a graph driving the rotation. The individual points look good-ish, but the actual spiral is way off in the model. I've done things like that with graphs before and the problem is the shape of the graph before and after the "points" you control, you just can't get what you want. And, you can't write a formula to control the graph itself inside of creo, though you MIGHT be able to write one in excel or something and import it. You MIGHT be able to do that trajectory as a curve via equation, but man, the math that would entail.....