Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Community
- Creo+ and Creo Parametric
- 3D Part & Assembly Design
- Straight beam limitations
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Straight beam limitations
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Straight beam limitations
Hi All,
This is not new but after staring long and hard at numbers that simply 'do not add up' when comparing beam and solid model results, I realise I have been here before.
So I thought I would share the following to help others avoid the same.
Beams are really useful, they reduce the size of a model, they are quick, we get bending moments, stresses etc.
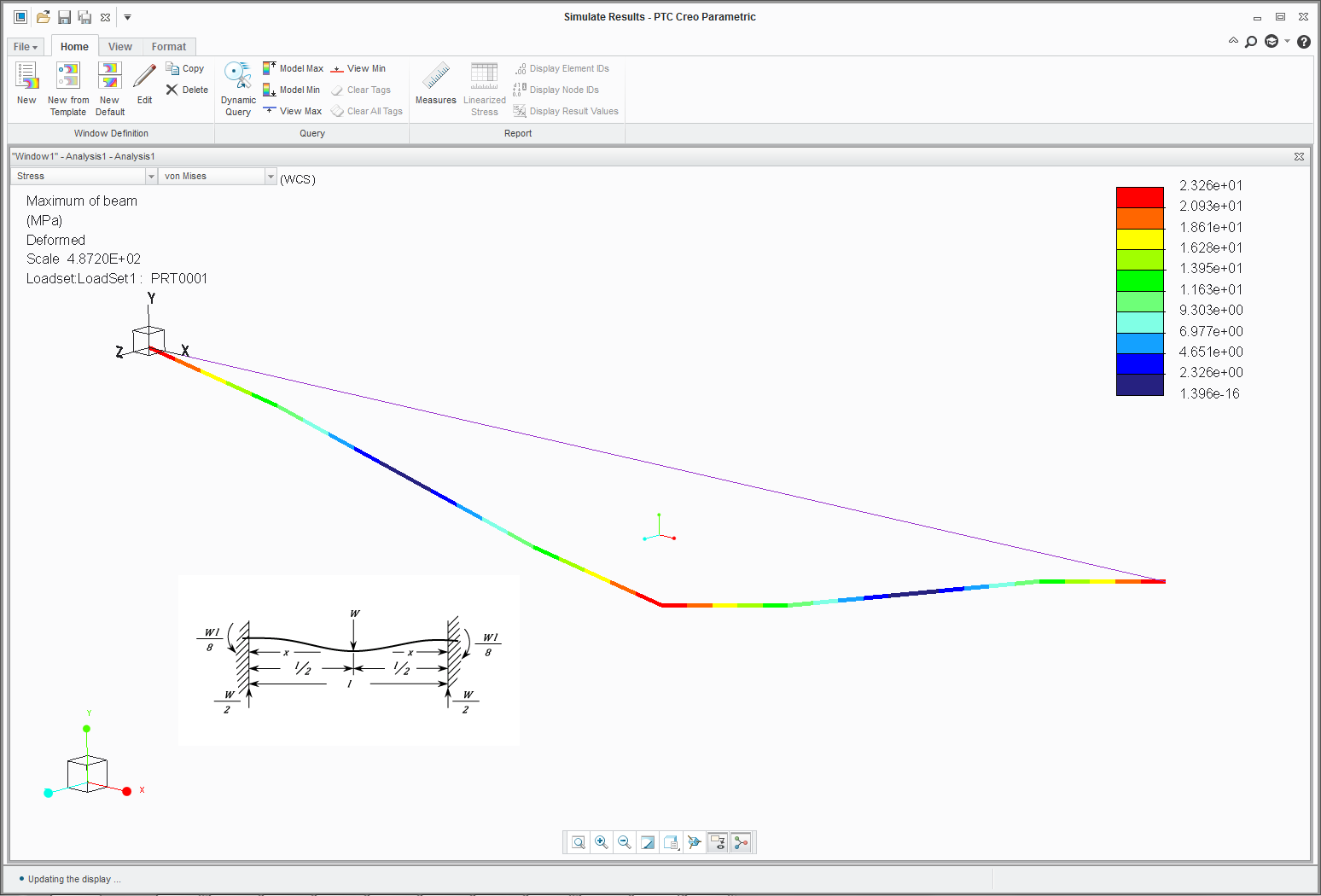
So consider the following simple model which approximates a built in I-beam loaded in the centre

It seems reasonably intuitive to me that as the beam is loaded, the constraints will be pulled toward each other and the constraints are acting to keep them where they begin means a horizontal reaction force.
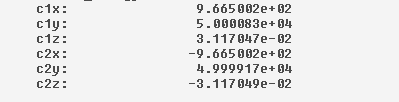
Define x,y,z, constraint reaction measures for C1 & C2 and we get the output :

The vertical load is shared equally (input 1e5N)
But no X-direction (horizontal) forces.
The deflected shape doesn't seem feel right either with it's abrupt change of curvature at centre span and the apparent lack of tangency to the horizontal at the built in ends.
What happens if we introduce a small kink in the original beam?

... Horizontal components appear

(the deflected shape still sees an abrupt change of curvature at centre span and lack of tangency with the horizontal at the ends)
In the first instance (straight beam) the applied force is normal to the to the beam. Small deflection theory = no horizontal force. (and a quick chat with a Civil confirmed that they generally only care about the moments and vertical forces at the supports)
In the second instance (deliberate kink) the structural stiffness is changed and horizontal components appear.
We now have to ponder whether these horizontal components are correct? Clearly if the 89.9deg figure is made 70deg say, the horizontal force will change. Therefore I have to answer : No, these horizontal component are probably quite wrong.
So off we go into Large Deflection Analysis world. There is no LDA for beam only models or models containing beams
Resorting to solid modelling (and ignoring the debate about how exactly the beam is built in, what the stiffness of the supports are, whether rotations are permitted within the support due to gaps, how is the load introduced etc. ; for this we keep it simple). Same model but solid and Small deflection theory


If we apply a bit of mesh control, 10% load steps and run LDA bearing in mind that it is the top flange that is bending a lot due to the concentrated load :
Conclusion : Beware horizontal beams lie.
Hope these ramblings make sense and are vaguely useful.
bfn
This thread is inactive and closed by the PTC Community Management Team. If you would like to provide a reply and re-open this thread, please notify the moderator and reference the thread. You may also use "Start a topic" button to ask a new question. Please be sure to include what version of the PTC product you are using so another community member knowledgeable about your version may be able to assist.
- Labels:
-
General
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"The deflected shape doesn't seem feel right either with it's abrupt change of curvature at centre span and the apparent lack of tangency to the horizontal at the built in ends."
How many "plotting grid" points do you have? The default of 4? Up that and those 'kinks' should go away.
As for the reason, this is a perfect example of the limitations of linear theory, and when one might need to go nonlinear.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Shaun,
Increasing the plotting grid density does not improve the picture. Neither does increasing the number of elements or forcing maximum edge order.
I think there are no horizontal forces because the moment at the support is a pure couple acting about the end point = no resultant
I have asked Tech support for their thoughts.
Thanks





